Kerasを使って活性関数・目的関数・最適化手法をまとめる（ディープラーニング）

まだ・・・何も分かっておらず、ディープラーニングで利用されている関数の概要を調べている程度です・・・。

LSTM（Long short-term memory）って何？
隠れ層・出力層における活性化関数
モデルをコンパイル

「KerasのFunctional API Modelの構造を理解する」の抜粋で、今回見ていくコードは次の部分です。

# LSTM を Keras を使って組む
def create_model():
    inputs = Input(shape=(10, 1))
    # 日経平均株価の値を直接予測するため活性化関数は linear
    # 中間層の数は 300（理由なし）
    x = LSTM(300, activation='relu')(inputs)
    price = Dense(1, activation='linear', name='price')(x)
    updown = Dense(1, activation='sigmoid', name='updown')(x)
    model = Model(inputs=inputs, outputs=[price, updown])
    # 後で検証に使用するため 2 値予測も含んでいる
    model.compile(loss={
        'price': 'mape',
        'updown': 'binary_crossentropy',
    }, optimizer='adam', metrics={'updown': 'accuracy'})
    return model

# LSTM を Keras を使って組む

def create_model():

inputs = Input(shape=(10, 1))

# 日経平均株価の値を直接予測するため活性化関数は linear

# 中間層の数は 300（理由なし）

x = LSTM(300, activation='relu')(inputs)

price = Dense(1, activation='linear', name='price')(x)

updown = Dense(1, activation='sigmoid', name='updown')(x)

model = Model(inputs=inputs, outputs=[price, updown])

# 後で検証に使用するため 2 値予測も含んでいる

model.compile(loss={

'price': 'mape',

'updown': 'binary_crossentropy',

}, optimizer='adam', metrics={'updown': 'accuracy'})

return model

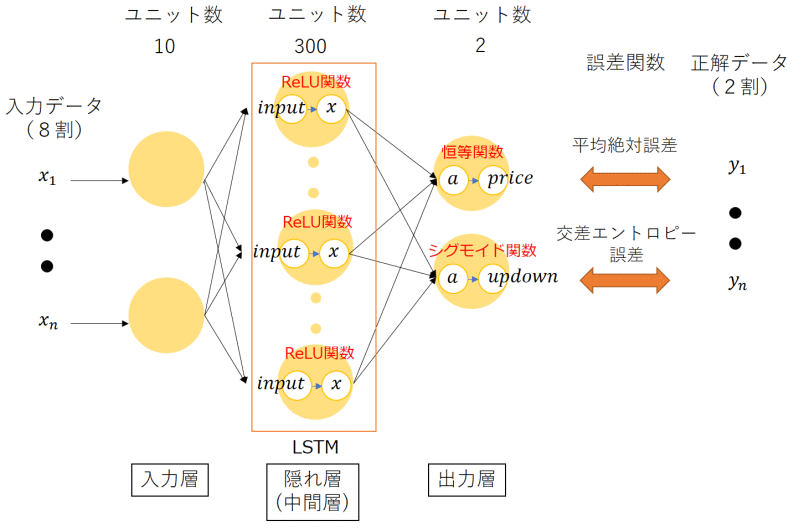
Kerasのgraphvizモジュールで学習モデルを可視化しましたが、よく分からないので自分なりに書き直してみました。

なんか違う気がするので誰か教えて下さい・・・。

LSTM（Long short-term memory）って何？

LSTMは1995年に登場しましたが、最近Google Voiceの基盤技術をはじめとした最先端の分野でも利用されるRNNです。

なら、RNN (再帰的型 Neural Network)って何？

RNNは以前に計算された情報を覚えるための記憶力を持っています。

ようするに例えば文章を予測したい場合、その前の言葉が何だったのかを知っておく必要があります。

そのような学習モデルを作るのに役立ちます。

最近では、従来のRNNの欠点を解消できる、より洗練されたRNNモデルも登場しています。

Bidirectional RNN：後の要素も計算に含める
Deep (Bidirectional) RNN：ステップごとに複数の層を持つ
LSTMネットワーク

最も使われているRNNの一つがLSTMです。

LSTMはRNNよりも距離のあるステップの関係性を学習するのに優れています（RNNは2,3ステップくらい前の情報しか覚えられません）。

・・・よく分からないので、ここも後学としてここでは単なる紹介としておきます。

隠れ層・出力層における活性化関数

    x = LSTM(300, activation='relu')(inputs)
    price = Dense(1, activation='linear', name='price')(x)
    updown = Dense(1, activation='sigmoid', name='updown')(x)

x = LSTM(300, activation='relu')(inputs)

price = Dense(1, activation='linear', name='price')(x)

updown = Dense(1, activation='sigmoid', name='updown')(x)

活性化関数（activation）

活性化関数は、入力信号の総和がどのように活性化するかを決定する役割を持ちます。

一般的に、ニューラルネットワークでは線形関数は使われません。

ソフトサイン（softsign：長・短期記憶で利用すると速く、飽和状態になる可能性が低下する）
ハイパボリックタンジェント（tanh：標準シグモイド関数を線形変換したもの）
シグモイド関数（sigmoid：入力した値が大きければ大きいほど1に近づき、入力した値が小さければ小さいほど0に近づく関数）
ハードシグモイド（hard_sigmoid）
ソフトプラス（softplus）
ランプ関数（relu：入力した値が0以下のとき0になり、1より大きいとき入力をそのまま出力）
線形関数・恒等関数（linear：入力した値と同じ値を常にそのまま返す関数）
ソフトマックス（softmax：分類の確信度が低くても総和が1になるよう補正する）

中間層では、とりあえずサチらない非線形関数、ReLUを使っておけばよい感じです。

最近はReLUよりもsoftplusやSwishで良い性能が出るという報告を見かけるようになっており、色々と更新が激しい分野です。

モデルをコンパイル

    model.compile(loss={
        'price': 'mape',
        'updown': 'binary_crossentropy',
    }, optimizer='adam', metrics={'updown': 'accuracy'})

model.compile(loss={

'price': 'mape',

'updown': 'binary_crossentropy',

}, optimizer='adam', metrics={'updown': 'accuracy'})

コンパイル時に最適化手法（optimizer）、損失関数（loss）、評価指標（metrics）を指定します。

最適化手法（optimizer）

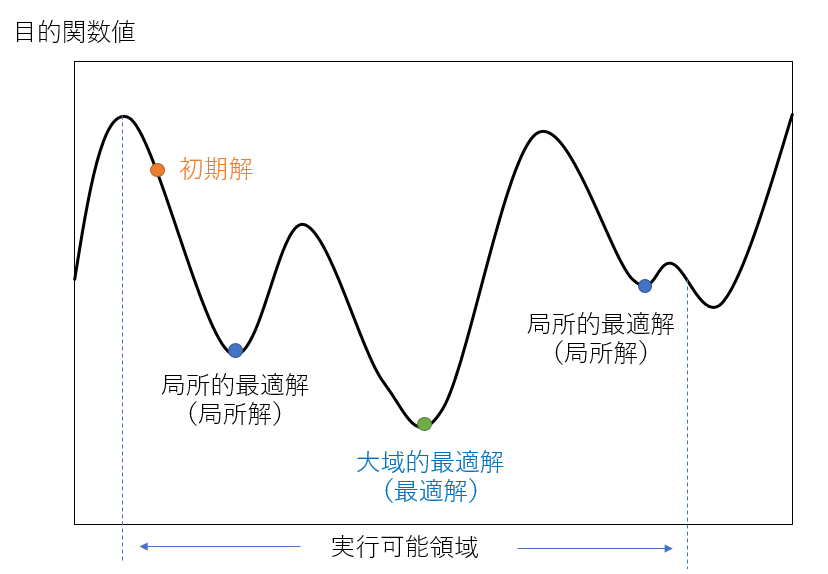
変数が増えるにつれ局所解が増えてしまい、最適解が得られなくなります。

そこで最適化手法の変動によって、新たなより適切な可能性のある「局所解」へ素早く移動することができます。

非線形関数の最小化手法の中では「勾配降下法」や「ニュートン法」が有名です。

ですが、収束が遅いため色々な手法が作られています。

確率的勾配降下法（sgd：Stochastic Gradient Descent）
rsmprop（2012年に Tijmen Tieleman らが発表した方法）
adagrad（2011年に John Duchi らが発表した方法）
adadelta（2012年に Matthew D. Zeiler が発表した方法）
adam（2015年に Diederik P. Kingma らが発表した方法）
adamax（2015年に Diederik P. Kingma らが発表した方法）
nadam（2016年、ネステロフの加速法を Adam に取り入れたもの）

一つ一つの式や特性に関しては今後少しずつ理解することにします。

目的関数（objective）⊃ コスト関数、誤差関数 = 損失関数（loss）

目的関数が最も大きな枠組みです。

つまり、コスト関数も誤差関数も損失関数も、目的関数です。

この関数（目的関数）を最小化させればモデルが導き出せる
この関数（目的関数）を最大化させればモデルが導き出せる

平均二乗誤差（mse：差の2乗の和）
平均絶対誤差（msa：差の絶対値の和）
平均絶対誤差率（mspa：差を正解の値で割った値（誤差率）の絶対値の和）
対数平均二乗誤差（msle：「1を加えた値の対数」の差の2乗の和）
ヒンジ損失の和（hinge）
ヒンジ損失の二乗の和（squared_hinge）
2クラス分類時の交差エントロピー（binary_crossentropy）
Nクラス分類時の交差エントロピー（categorical_crossentropy）
スパースなNクラス分類交差エントロピー（sparse_categorical_crossentropy）
KLダイバージェンス（kld）
poisson
コサイン類似度を負にしたもの（cosine_proximity）

一つ一つの式や特性に関しては今後少しずつ理解することにします。

評価指標（metrics）

代表的な評価指標は次の通りです。

正確度 (正解率、Accuracy：推定した値と真の値が一致した割合)
適合率 (精度、陽性反応的中度、Precision：正確性を見るための指標)
再現率 (感度、真陽性率、Recall：網羅性を見るための指標)
F-値 (F-score, F-measure)
AUC (Area Under the Curve)

一般的にはAccuracyを使っていれば問題ないようです。

一つ一つの式や特性に関しては今後少しずつ理解することにします。

何となくだけど、モデルの作り方・関数の指定方法は分かりはじめてきました。

どのようなモデルして、どの関数を使うか？ユニット数をいくつにするか？そして、どのような入力データを与えるか？が難しいのだろうね。

って、全てだな・・・。

ディープラーニングを学習するには、この本がオススメです。