今回も、kaggleの入門者向けチュートリアルコンペ「住宅価格予測」を解いてみます。
House Prices: Advanced Regression Techniques
各種指標を用いて住宅の価格を予測する分析問題です。
- 【6回目】KaggleのHouse Pricesで回帰分析(EDA:Exploratory Data Analysis編)
- 【5回目】Kaggle の Titanic Prediction Competition でクラス分類(XGBoost、LightGBM、CatBoost編)
- 【4回目】Kaggle の Titanic Prediction Competition でクラス分類(scikit-learn編)
- 【3回目】Kaggle の Titanic Prediction Competition でクラス分類(Keras Functional API編)
- 【2回目】Kaggle の Titanic Prediction Competition でクラス分類(Jupyter Notebook編)
- 【1回目】Kaggle の Titanic Prediction Competition でクラス分類(Keras導入編)
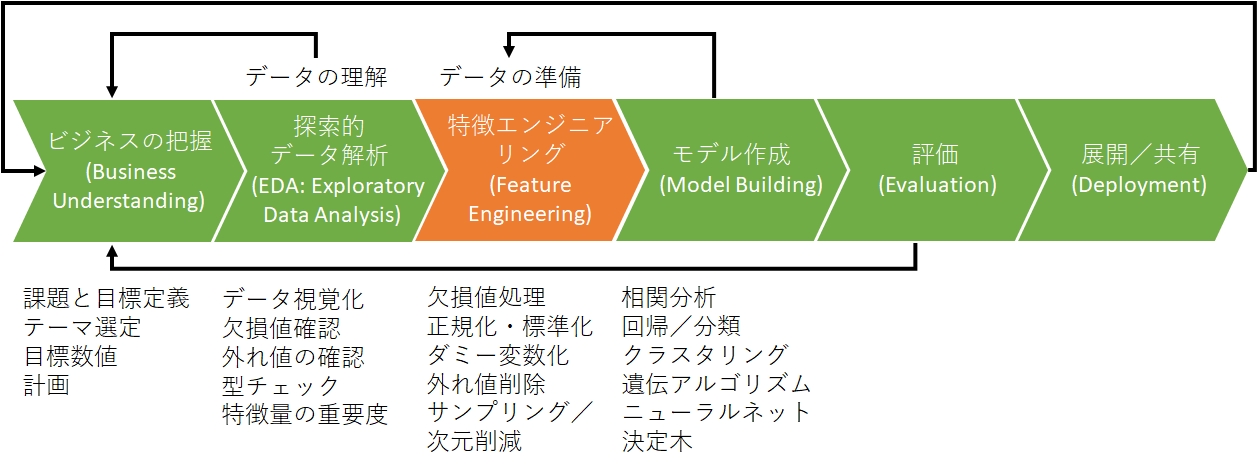
データ分析のプロセスとして、CRISP-DM(CRoss Industry Standard Process for Data Mining)というものがあります。
モデリングより前のステップである「ビジネスの理解」「データの理解(Exploratory Data Analysis)」「データの準備(Feature Engineering)」のステップが大半を占めます。
今回はタイタニックに続いて二度目の「データの準備(Feature Engineering)」という位置付けです。
Python命名規則一覧
PEP8でPython命名規則が次のように定められています。
| 対象 | ルール | 例 |
|---|---|---|
| パッケージ | 全小文字 なるべく短くアンダースコア非推奨 | tqdm, requests … |
| モジュール | 全小文字 なるべく短くアンダースコア可 | sys, os,… |
| クラス | 最初大文字 + 大文字区切り | MyFavoriteClass |
| 例外 | 最初大文字 + 大文字区切り | MyFuckingError |
| 型変数 | 最初大文字 + 大文字区切り | MyFavoriteType |
| メソッド | 全小文字 + アンダースコア区切り | my_favorite_method |
| 関数 | 全小文字 + アンダースコア区切り | my_favorite_funcion |
| 変数 | 全小文字 + アンダースコア区切り | my_favorite_instance |
| 定数 | 全大文字 + アンダースコア区切り | MY_FAVORITE_CONST |
前回、行列を「X_test」と表したので全小文字を守ってませんが、それ以外は従って記載します。
特徴エンジニアリング(データの準備:前処理)
次のようなことを行います。
- 外れ値の除去(.drop)
- 外れ値・多重共線性の変数除去
- 欠損値の補完または除去(pandasの.fillna())
- 数値型特徴のカテゴリ変数化
- ダミー化(ラベル&ワンホットエンコーディング)(pandasの.get_dummies())
- 数値変数をモデルに適した形式へ変換(対数変換、BoxCox変換)
- 数値型特徴の正規化と標準化
- 次元削減と特徴量抽出
- 学習データとテストデータをマージする
- カテゴリ型特徴の組み合わせ特徴生成
データの読み込み
|
1 2 3 4 5 6 7 8 |
import pandas as pd # CSV読み込み df_train = pd.read_csv("train.csv") df_test = pd.read_csv("test.csv") #それぞれのデータのサイズを確認 print("df_train: "+str(df_train.shape)) print("df_test: "+str(df_test.shape)) |
|
1 2 |
df_train: (1460, 81) df_test: (1459, 80) |
外れ値・多重共線性の変数除去(.drop)
統計学において、他の値から大きく外れた値のことを外れ値と言います。
「多重共線性」も除去が必要なため、相関の高い変数をまとめた新変数に対して、外れ値を確認して除去します。
- OverallQualが10より小さくSalePriceが500000より大きい場合は除去
- OverallQualが5より小さくSalePriceが200000より大きい場合は除去
- TotalSF(1stFlrSF+2ndFlrSF+TotalBsmtSF+GrLivArea)が10000より大きく、SalePriceが300000より小さい場合は除去
- SF(WoodDeckSF+OpenPorchSF+BsmtFinSF1)のSalePriceが500000より大きい場合は除去
- Garage(GarageCars+GarageArea)のSalePriceが500000より大きい場合は除去
- Year(YearBuilt+YearRemodAdd)のSalePriceが500000より大きい場合は除去
- それ以外の変数のSalePriceが600000より大きい場合は除去
物件の大きさ(広さ)の外れ値を除去します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 外れ値の削除 def del_outlier(df): df = df.drop(df[(df["TotalSF"]>10000) & (df["SalePrice"]<300000)].index) for col in df: if df[col].dtype != "object" and col != "SalePrice": df = df.drop(df[(df[col]>=0) & (df["SalePrice"]>600000)].index) df = df.drop(df[(df["OverallQual"]<10) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["OverallQual"]<5) & (df["SalePrice"]>200000)].index) df = df.drop(df[(df["SF"]>=0) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["Garage"]>=0) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["Year"]>=0) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["Year"]<3900) & (df["SalePrice"]>400000)].index) return df # 多重共線性の削除 def del_multicollinearity(df): df["Garage"] = df["GarageCars"] + df["GarageArea"] df["Year"] = df["YearBuilt"] + df["YearRemodAdd"] df["SF"] = df["WoodDeckSF"] + df["OpenPorchSF"] df["TotalSF"] = df["1stFlrSF"] + df["2ndFlrSF"] + df["TotalBsmtSF"] + df["GrLivArea"] # カラム削除 cols = ["GarageCars","GarageArea","1stFlrSF", "2ndFlrSF", "TotalBsmtSF", "GrLivArea", "YearBuilt", "YearRemodAdd", "WoodDeckSF", "OpenPorchSF"] for i in cols: df = df.drop(i, axis=1) return df |
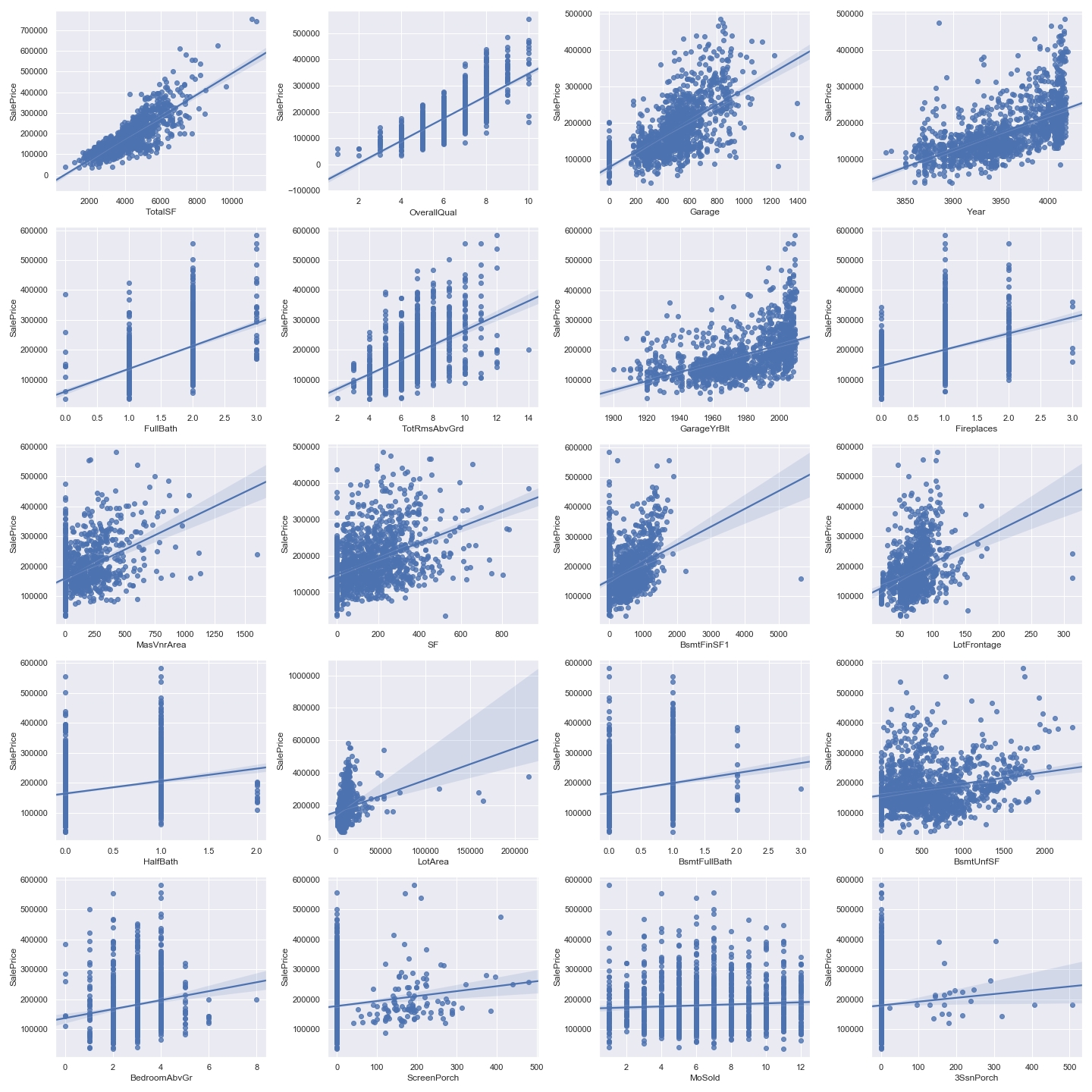
その上で、散布図を出力してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
sns.set() df_train = del_multicollinearity(df_train) df_train= del_outlier(df_train) df = df_train # number of variables for heatmap k = 21 fig = plt.figure(figsize=(20,20)) # 各列の間の相関係数算出 corrmat = df.corr() # リストの最大値から順にk個の要素を取得 cols = corrmat.nlargest(k, "SalePrice")["SalePrice"].index # NumPyの相関係数を求める(最初はSalePriceなので不要) for i in np.arange(1,k): X_train = df[cols[i]] ax = fig.add_subplot(5,4,i) # 図やサブプロットのうち一番最後のものに描画 sns.regplot(x=X_train, y=y_train) plt.tight_layout() plt.show() fig.savefig("figure7.png") |
大きな外れ値は除去されました。
欠損値の補完または除去(pandasの.fillna())
欠損値の除去の手法一覧は次の通りです。
|
1 2 3 4 5 6 7 8 |
# 欠損値を含む"行"を削除 df = df.dropna() # 欠損値を含む"列"を削除 df = df.dropna(axis=1) # 指定した列の欠損値が含まれている行だけを削除 df = df.dropna(subset=['列名']) # 指定した列だけを抽出(リストをネストするのがポイント) df = df[["列名","列名"]] |
欠損値の補完の手法一覧は次の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 0で埋める場合 df = df.fillna(0) # 文字で埋める場合 df = df.fillna('任意の文字列') # 列を選んで適用することも可能 df['列名'] = df['列名'].fillna(0) # 欠損値を列の平均値で埋める df = df.fillna(df.mean()) # 欠損値を列の中央値で埋める df = df.fillna(df.median()) # 欠損値を列の最頻値で埋める df = df.fillna(df.mode()) # 欠損値を列の1つ手前の値で埋める df = df.fillna(method='ffill') # 欠損値を列の直後の値で埋める df = df.fillna(method='bfill') # 列ごとに指定の値で欠損値を埋める df = df.fillna({'列名1': 0, '列名2': 5000, '列名3': 35}) # 列方向に推測したデータを入れたいときは df = df.interpolate() # 行方向に推測したデータを入れたいときは df = df.interpolate(axis=1) |
データフレームから特定の行や列を取得する手法一覧は次の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# A列をSeriesとして取り出す df = df["A"] # A列をSeriesとして取り出す df = df.A # 0~2行目 df = df[0:2] # 0~3行目 df = df[:3] # Alpha~Betaの行を取り出す df = df["Alpha":"Beta"] # Betaの行を取り出す df = df.loc["Beta"] # AとBの列を取り出す df = df.loc[:, ["A", "B"]] # Alpha~Betaの行のAとB df = df.loc["Alpha":"Beta",["A", "B"]] # 0行目 df = df.iloc[0] # 1行目の1列目 df = df.iloc[1][1] # 1, 2行目の0, 1列 df = df.iloc[[1, 2],[0, 1]] # 1~2行目のすべての列 df = df.iloc[1:2, :] # すべての行の0~1列 df = df.iloc[:, 0:1] # Alphaの行のB df = df.at["Alpha", "B"] # 1行目の2列目 df = df.iat[1, 2] # Aの値が5より大きいすべての行 df = df[df.A > 5] # 5より大きいすべての要素、他はNaN df = df.[df > 5] # A列に 1 または 1000 の値を持つ行。※isinの引数はリスト型 df = df[df["A"].isin([1, 1000])] |
またlambda(無名関数)を使って「ある変数のカテゴリの中央値で補完する」という柔軟な記載方法もできます。
|
1 2 3 4 5 6 7 8 |
df = pd.DataFrame({ 'city': ['osaka', 'osaka', 'osaka', 'osaka', 'tokyo', 'tokyo', 'tokyo'], 'food': ['apple', 'orange', 'banana', 'banana', 'apple', 'apple', 'banana'], 'price': [100, 200, 250, 300, 150, None, 400], 'quantity': [1, 2, 3, 4, 5, 6, 7] }) df['price'] = df.groupby('food')['price'].transform(lambda x: x.fillna(x.median())) df |
今回のデータに対してはデータの欠損そのものが情報だと分かっているので、次のような方針で補完します。
- カテゴリカル変数(object)の欠損:欠損を示す文字列「NA」を補完
- 数値型変数(float)の欠損「0.0」を補完
- LotFrontage(隣接した道路の長さ)は、Neighborhood(同じ地区)の他の物件の「中央値」を補完
Neighborhood(Ames市域内の物理的な場所)には、Blmngtn(ブルーミントンハイツ)、Blueste(ブルーステム)、BrDale(ブライアデール)、BrkSide(ブルックサイド)、ClearCr(クリアクリーク)などの値が入っています。
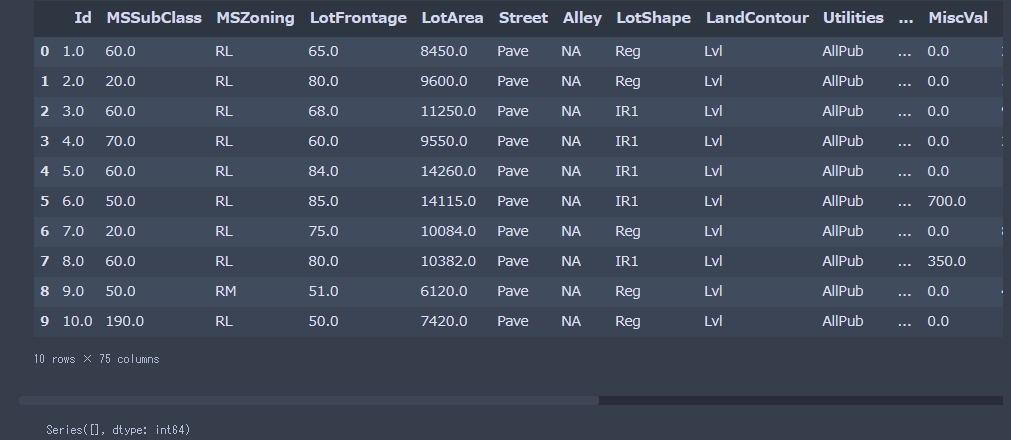
欠損値の補完は次のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 欠損値補完 def do_imputation(df): df['LotFrontage'] = df.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median())) for col in df: #check if it is a number if df[col].dtype != "object": df[col].fillna(0.0, inplace=True) else: df[col].fillna("NA", inplace=True) return df df = do_imputation(df) display(df.head(10)) # 学習データの欠損状況 df.isnull().sum()[df.isnull().sum()>0].sort_values(ascending=False) |
欠損データは無くなりました。
数値型特徴のカテゴリ変数化
データの型は「数値」でも、数値の大きさに意味を持たない(1と10で比較した場合、10倍の違いがない)場合、カテゴリ変数に変換します。
| 尺度 | 説明 |
|---|---|
| 名義尺度 | 識別のために数字を与えたもの。例えばID、電話番号など。LabelEncoderで変換される整数値を用いて回帰分析を行うことはできない。1つの変数の離散値として扱う場合は、決定木分析、ランダムフォレストなどの分析と相性が良い |
| 順序尺度 | 順序を表す数字。例えばランキング、地震の震度、成績表などが。数字の大小に意味はあるが、差や比は意味がない。ラベルと整数を対応させるディクショナリを使って、マッピングを行うことで数値化 |
| 間隔尺度 | 間隔に意味のある数値。例えば℃単位の温度。「夏の最高気温30℃は春の最高気温15℃より2倍大きい」と言うことに意味はないが、「夏の一日の寒暖差(最高気温と最低気温の”間隔”)6℃は、春の寒暖差12℃より2倍小さい」と言うことは可能 |
| 比例尺度 | 四則演算が全て使える数値。温度も絶対温度K(ケルビン)に直せば比例尺度になる。年齢、金額、期間などもこれに属す |
機械学習においては数式上で四則演算を行うので、全ての値を比例尺度に変換するのが好ましいです。
データの定義を見てみると、以下の変数は数値変数ではなくカテゴリ変数として扱ったほうが良さそうです。
| 変数名 | 説明 |
|---|---|
| MSSubClass: Identifies the type of dwelling involved in the sale | 住宅の種類を表す。数値はどの種類に当てはまるかを表すだけで大きさや順序に意味はない |
| YrSold: Year Sold (YYYY) | 販売年。大きさや順序に意味はない |
| MoSold: Month Sold (MM) | 販売月。大きさや順序に意味はない |
|
1 2 3 4 5 6 7 8 9 10 |
# 数値変数のカテゴリ変数化 def change_num_to_str(df): # MSSubClass=The building class df["MSSubClass"] = df["MSSubClass"].apply(str) # Changing OverallCond into a categorical variable df['OverallCond'] = df["OverallCond"].astype(str) # Year and month sold are transformed into categorical features. df["YrSold"] = df["YrSold"].astype(str) df["MoSold"] = df["MoSold"].astype(str) return df |
※最終的には、学習データとして価値が無さそうなので除去しました(以下参照)。
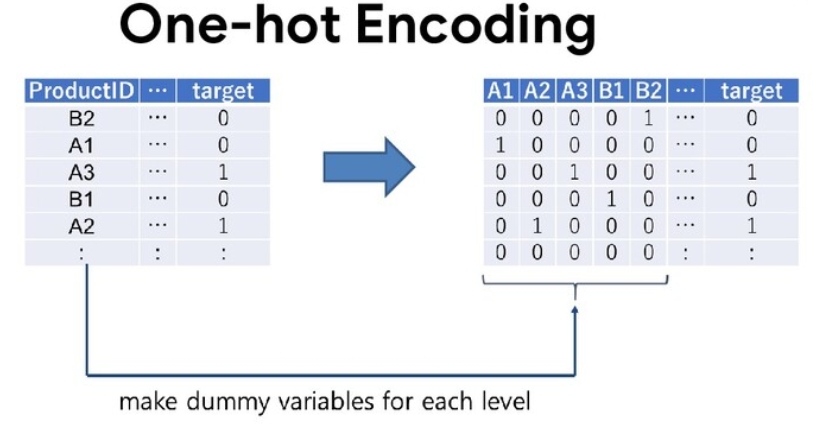
カテゴリカル変数のエンコーディング(ダミー変数)
文字列でカテゴリー分けされた性別などのデータを、男を0, 女を1のように変換したり、多クラスの特徴量をone-hot表現に変換することをエンコーディング(ダミー変数)と呼びます。
次の手法がよく使われています。
- Label encoding
- Count encoding (frequency encoding)
- One-hot encoding
- Target encoding
- Lightgbm の categorical feature support
- Catboost の ordered target encoding
Kaggleではlabel encodingが人形です(one-hot encodingの方がパフォーマンスが高い)。
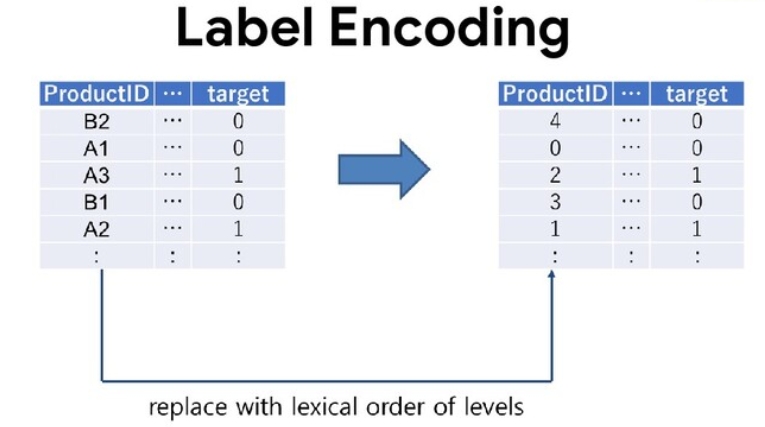
Label encoding
Label encodingは、決定木ベースのアルゴリズムで有効でカテゴリカル変数をスカラ値(数値)に変換します。
|
1 2 3 4 5 6 7 8 9 |
# string label to categorical values from sklearn.preprocessing import LabelEncoder for i in range(df.shape[1]): # iloc(行番号, 列番号) if df.iloc[:,i].dtypes == object: lbl = LabelEncoder() lbl.fit(list(df.iloc[:,i].values)) df.iloc[:,i] = lbl.transform(list(df.iloc[:,i].values)) |
One hot Encoding
一方、One hot Encodingにより、カテゴリカル変数に対して、各要素が該当するなら1、該当しないなら0とするカラムを変数の要素数分作ることができます。
One Hot Encodingであれば決定木ベースや線形回帰やニューラルネットでも有効に作用します。
一般的には「get_dummies」などを利用します。
|
1 2 3 4 |
# カテゴリカル変数をダミー変数化(NaNもダミー化) df= pd.get_dummies(df["col"], dummy_na=True) # 自分でダミー変数を作る adult = (df['age'] >= 20).astype(np.int64) |
ラベルエンコーディングでは発生頻度の低い稀なカテゴリなどが取りにくく、重要な変数がうまく取れない場合があるため、One hot encodingはの処理に役立ちます。
ただし、データ量が多い場合にはかなりのメモリ消費を強いられます。
このため、扱うアルゴリズムに応じて適切なEncodingを使わなくてはいけません。
その他のEncoding
各変数の順序関係に従って、エンコーディングする場合は、次のように記載できます。
|
1 2 3 4 5 6 7 |
for i in df.loc[:, df.dtypes == 'object'].columns: num=-1 mapping={} for j in df.groupby(i)['SalePrice'].mean().sort_values().index: num+=1 mapping[j]=num df[i]= df[i].map(mapping) |
int64、float64は数値なので、そのままモデルに投げることができます。
ただ、objectは基本的には文字情報で、このままだとモデルに与えることはできません。
まずobject変数を抽出し、それぞれの意味を確認します。
|
1 2 3 |
for col, item in df.iteritems(): if item.dtypes == object: print(col + "\t" + str(item.dtypes)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
MSZoning object 一般的なゾーニング分類。8種類に分類される LandContour object 物件の平坦度。4種類に分類される Utilities object 利用可能なユーティリティ。4種類に分類される LotConfig object ロット構成。5種類に分類される Neighborhood object Ames市域内の物理的な場所 Condition1 object 幹線道路または鉄道への近さ。9種類に分類される Condition2 object 幹線道路または鉄道への近さ(複数ある場合)。9種類に分類される BldgType object 住居の種類。種類に分類される HouseStyle object 住まいのスタイル。4種類に分類される RoofStyle object 屋根の種類。6種類に分類される RoofMatl object 屋根材。8種類に分類される Exterior1st object 家の外装。17種類に分類される Exterior2nd object 家の外装材(複数の素材がある場合)。17種類に分類される MasVnrType object 石積みのベニヤタイプ。5種類に分類される Foundation object 基礎、基盤の種類。6種類に分類される Heating object 暖房の種類。6種類に分類される Electrical object 電気システム。5種類に分類される GarageType object 車庫の場所。7種類に分類される MiscFeature object 他のカテゴリに含まれていないその他の機能。6種類に分類される SaleType object 販売の種類。10種類に分類される SaleCondition object 販売条件。6種類に分類される |
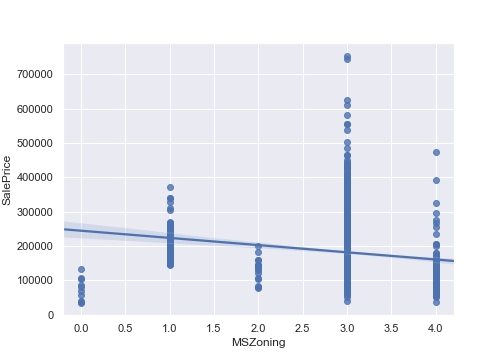
ひとつひとつカラムをラベルエンコーディングで数値化しながら確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# ラベルエンコーダー def encode_label(df, i): lbl = LabelEncoder() lbl.fit(list(df[i].values)) df[i] = lbl.transform(list(df[i].values)) return df[i] i = "MSZoning" tmp = encode_label(df, i) fig = plt.figure(figsize=(7,5)) sns.regplot(x=tmp, y=df["SalePrice"]) plt.xlabel(i) plt.ylabel("SalePrice") plt.show() fig.savefig("figure8.png") |
順序に意味がない名義尺度では、LabelEncoderで変換される整数値を用いて回帰分析を行うことはできません。
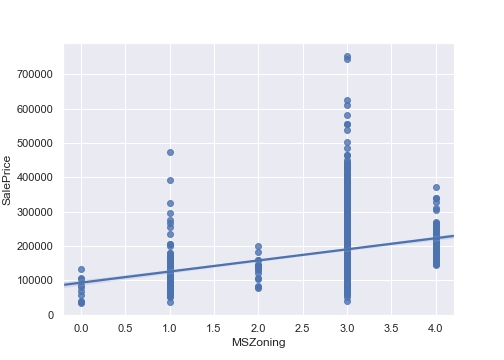
これを、順序尺度の性質を持つように「SalePrice」でエンコーディングしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
i = "MSZoning" num=-1 mapping={} for j in df.groupby(i)['SalePrice'].mean().sort_values().index: num+=1 mapping[j]=num df[i]= df[i].map(mapping) fig = plt.figure(figsize=(7,5)) sns.regplot(x=df[i], y=df["SalePrice"]) plt.xlabel(i) plt.ylabel("SalePrice") plt.show() fig.savefig("figure9.png") |
今回は、他も同じようにエンコーディングします。
変数の除去(pandasの.drop())
変数の除去の手法一覧は次の通りです。
|
1 2 |
# 指定した列をまるごと除去 df = df.drop("列名", axis=1) |
他の変数は特徴量を減らすため、利用せず除去します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 不要変数の削除 def del_variable(df): cols = ("MSSubClass", "OverallCond", "YrSold", "MoSold", "Id", "LandContour", "Utilities", "LotConfig", "Neighborhood", "Condition1", "Condition2", "BldgType", "HouseStyle", "RoofStyle", "RoofMatl", "Exterior1st", "Exterior2nd", "MasVnrType", "Foundation", "Heating", "Electrical", "GarageType", "MiscFeature", "SaleType", "SaleCondition") for i in cols: df = df.drop(i, axis=1) return df df_train = del_variable(df_train) df_test = del_variable(df_test) df_train.dtypes.value_counts() |
|
1 2 3 |
float64 26 int64 24 dtype: int64 |
object変数は除去されました。
数値変数をモデルに適した形式へ変換
数値データは多くの問題を抱えています。
- スケールが大きく異なる
- 歪んだ分布をもつ
- 大小の外れ値を含む
- 変数間で、線形では表現できないような複雑な関係を持っている
- 冗長な情報
これらの問題は、回帰か分類かという課題設定に応じて、適用するモデルの種類によって顕在化します。
k近傍法やサポートベクターマシンは、特徴空間上の外れ値の影響を受けやすい性質があります。
一方で、実際の値ではなく順位化されたデータを利用する木ベースのモデルでは外れ値の影響を軽減可能です。
線形回帰モデルでは、出力から得られる値の誤差が正規分布に従うことを仮定します。
そのため正規分布とは異なる形状の分布をもつデータ(例えば離散値)では、その仮定が成立しない可能性があります。
このような状況では部分最小二乗法を用いることで説明変数の相関を無相関化できます。
そのための手法として次のようなものがあります。
| 変換方法 | 説明 |
|---|---|
| スケール変換 | データが取りうる値のスケールを変換し、一定の範囲に収める処理を行う |
| 対数変換 | 特徴量のスケールが大きい時はその範囲を縮小し、小さい時は拡大する。分散が大きなデータでは平均値が大きいほど等分散となりやすい傾向がある。0や負値を扱えない(下駄を履かせる必要あり) |
| Box-Cox変換 | データの分布を変えることでデータを正規分布に近づける。0や負値を扱えない(下駄を履かせる必要あり) |
| Yeo-Johnson変換 (Yeo-Johnson Power Transformations) | 0や負値を含んだ特徴量を扱える |
| ロジット変換 | 0から1の値を負と正の無限大の間の値に変換。つまり変換後の値は正規分布に近づく |
対数変換を利用する場合
対数変換では、変数 x を自然対数 log e_x に変換することを指します。
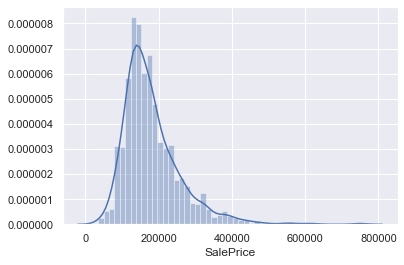
まずはグラフを再確認します。
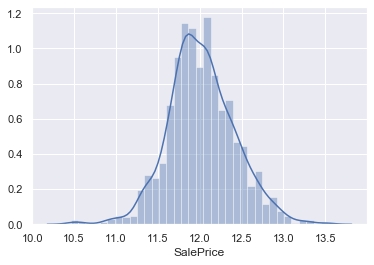
|
1 2 3 4 |
sns.distplot(df['SalePrice']) #歪度と尖度を計算 print("歪度: %f" % df['SalePrice'].skew()) print("尖度: %f" % df['SalePrice'].kurt()) |
|
1 2 |
歪度: 1.882876 尖度: 6.536282 |
歪度が正の値なので、右裾が長い(≒左に偏っている)分布であること、尖度が正の値のため正規分布よりもだいぶ尖った(平均付近にデータが集中している)分布であることがわかります。
次に、logを使って対数変換をすることで正規分布に近づけます。
|
1 |
sns.distplot(np.log(df['SalePrice'])) |
学習モデルで予測後は、expを使って元のスケールに戻すことを忘れないでください。
|
1 |
y_pred = np.exp(reg.predict(X_test)) |
Box-Cox変換・Yeo-Johnson変換を利用する場合
同様に大きく歪んだ特徴量は、Box-Cox変換を使って補正することもできます。
Box-Cox変換とは、変数のスケールを変えて分布を正規分布(ガウス分布)の形に変えてくれる変換です。
|
1 2 3 4 5 6 7 8 9 |
# 歪度0.5以上の特徴量に対して補正 skewness = skewness[abs(skewness) > 0.5] from scipy.special import boxcox1p skewed_features = skewness.index lam = 0.15 # 定数0.15を利用 for feat in skewed_features: #all_data[feat] += 1 df[feat] = boxcox1p(df[feat], lam) |
Box-Cox変換は0以下の値をとる変数には使用できないため、まずは各変数の最小値を確認します。
|
1 2 |
for i in df_train: print(str(min(df_train[i])) + "\t" + str(i)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
0 MSZoning 0.0 LotFrontage 0 LotArea 0 Street 0 Alley 0 LotShape 0 LandSlope 0 OverallQual 0.0 MasVnrArea 0 ExterQual 0 ExterCond 0 BsmtQual 0 BsmtCond 0 BsmtExposure 0 BsmtFinType1 0 BsmtFinSF1 0 BsmtFinType2 0 BsmtFinSF2 0 BsmtUnfSF 0 HeatingQC 0 CentralAir 0 LowQualFinSF 0 BsmtFullBath 0 BsmtHalfBath 0 FullBath 0 HalfBath 0 BedroomAbvGr 0 KitchenAbvGr 0 KitchenQual 0 TotRmsAbvGrd 0 Functional 0 Fireplaces 0 FireplaceQu 0.0 GarageYrBlt 0 GarageFinish 0 GarageQual 0 GarageCond 0 PavedDrive 0 EnclosedPorch 0 3SsnPorch 0 ScreenPorch 0 PoolArea 0 PoolQC 0 Fence 0 MiscVal 34900 SalePrice 0 Garage 0 Year 0 SF 0 TotalSF |
負の値はないですが、0が含まれる変数が多くあります。
今回はBox-Cox変換ではなく、0以下の値を持つ変数にも適用可能なYeo-Johnson変換を使うことにします。
|
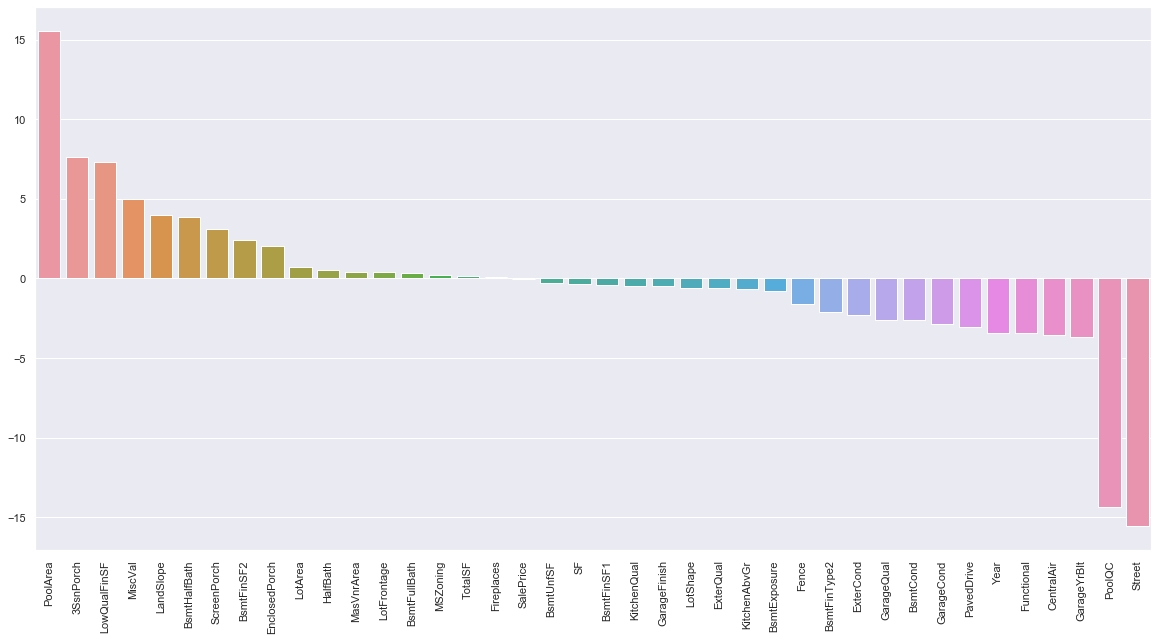
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
from sklearn.preprocessing import PowerTransformer def num_skew(df): # 数値の説明変数のリストを作成 num_feats = df.dtypes[df.dtypes != "object" ].index # 各説明変数の歪度を計算 skewed_feats = df[num_feats].apply(lambda x: x.skew()).sort_values(ascending = False) # 歪度の絶対値が0.5より大きい変数だけに絞る skewed_feats_over = skewed_feats[abs(skewed_feats) > 0.5].index # 各変数の最小値を表示 # for i in skewed_feats_over: # print(str(min(df[i])) + "\t" + str(i)) return skewed_feats, skewed_feats_over #Yeo-Johnson変換 def trans_yeo_johnson(df, skewed_feats_over): pt = PowerTransformer() pt.fit(df[skewed_feats_over]) #変換後のデータで各列を置換 df[skewed_feats_over] = pt.transform(df[skewed_feats_over]) #各説明変数の歪度を計算 skewed_feats_fixed = df[skewed_feats_over].apply(lambda x: x.skew()).sort_values(ascending = False) return skewed_feats_fixed skewed_feats, skewed_feats_over = num_skew(df_train) skewed_feats_fixed = trans_yeo_johnson(df_train, skewed_feats_over) #グラフ化 plt.figure(figsize=(20,10)) plt.xticks(rotation='90') sns.barplot(x=skewed_feats_fixed.index, y=skewed_feats_fixed) |
この変換も奥が深いので、詳細はまた今度調査します。
新たな特徴量の追加
SalesPriceを予測する「Zillow Prize: Zillow’s Home Value Prediction」で、
物件の面積を部屋数で割った1部屋当たりの面積という特徴量を追加したことで精度が上がった
[引用] 新たな特徴量の追加
という記事を見つけたので追加してみます。
|
1 2 |
# 特徴量に1部屋あたりの面積を追加 df["FeetPerRoom"] = df["TotalSF"]/df["TotRmsAbvGrd"] |
数値型特徴の標準化や正規化
木ベースのモデル(決定木、ランダムフォレスト)では、特徴量を入力とする複数のステップ関数(閾値を超えた場合に1, そうでなければ0に変換する)の組み合わせによって構成されるため変数のスケールの影響を受けません。
ロジスティック回帰や部分最小二乗法、リッジ回帰や距離を利用するk-means、主成分分析など、多くのモデルは入力のスケールに敏感で、変数間のスケールを揃える必要があります。
リッジ回帰、主成分分析では入力に用いる変数間のスケールが標準化されていることが前提です。それは特徴量空間におけるデータ間を距離を利用するためです。
そのため、標準化したデータを元に主成分分析を行う必要があります。
| 手法 | 内容 |
|---|---|
| 標準化 (standardization) | とは、平均0、分散(標準偏差)1にすること |
| 正規化 (normalization) | 取りうる値の範囲が統一すること |
体重や身長など、単位が異なる変数を比較する際に役立ちます。
[EDA] 決定木による相関の強い特徴量チェック(feature_importance_)
欠損値が無くなり数値化されたので、sklearnのランダムフォレストのfeature_importance_を見ることにより、どのFeatureがどれくらい重要か見てみましょう。
【matplotlibの場合】
|
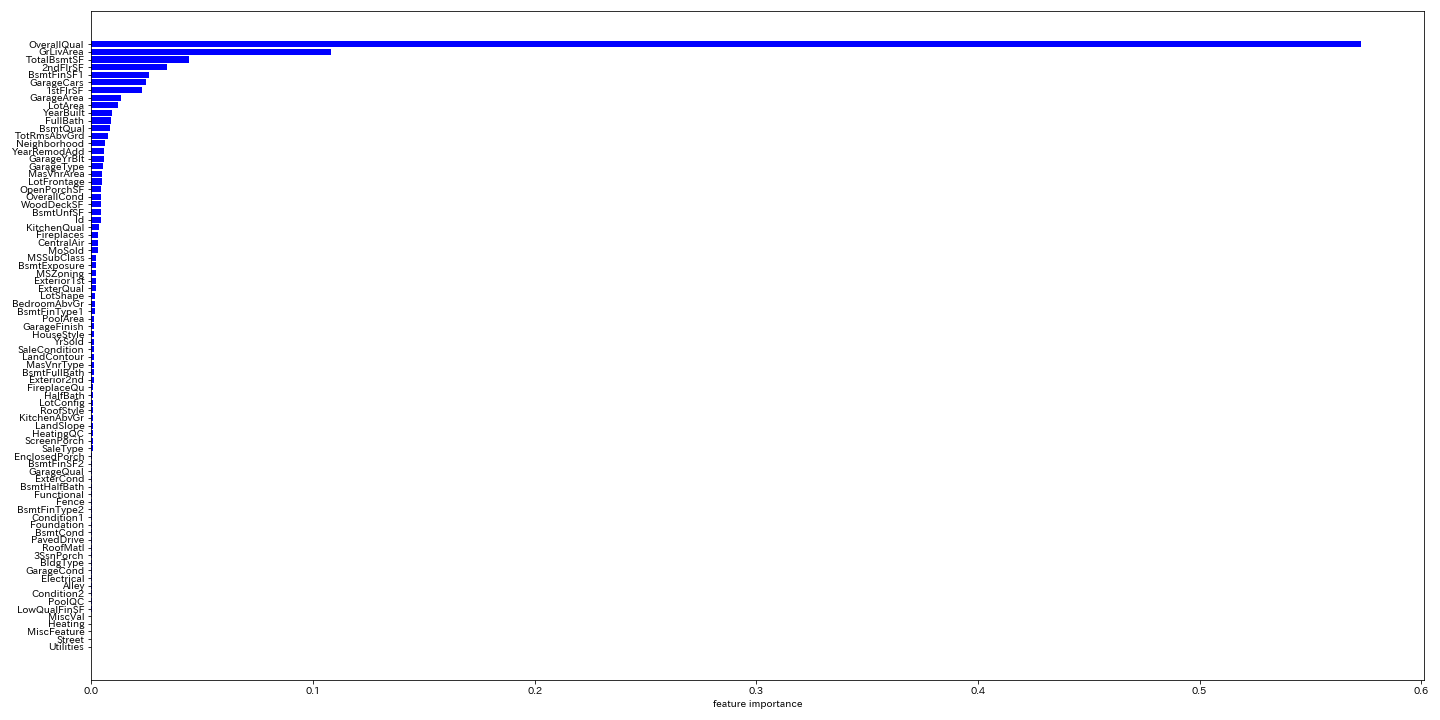
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# ランダムフォレスト def do_RandomForestRegressor(df): y_train = df['SalePrice'] X_train = df.drop(['SalePrice'], axis=1) rf = RandomForestRegressor() rf.fit(X_train, y_train) ranking = np.argsort(rf.feature_importances_) fig, ax = plt.subplots(figsize=(20, 10)) plt.barh(range(len(ranking)), rf.feature_importances_[ranking], color='b') plt.yticks(range(len(ranking)), X_train.columns[ranking]) ax.set_xlabel("feature importance") plt.tight_layout() plt.show() fig.savefig("figure.png") # CSV読み込み df_train = pd.read_csv("train.csv") for col in df_train: #check if it is a number if df_train[col].dtype != "object": df_train[col].fillna(0.0, inplace=True) else: df_train[col].fillna("NA", inplace=True) # 数値型の列のみ取り出すメソッド(public ではない) df_train = df_train._get_numeric_data() do_RandomForestRegressor(df_train) |
【seabornの場合】
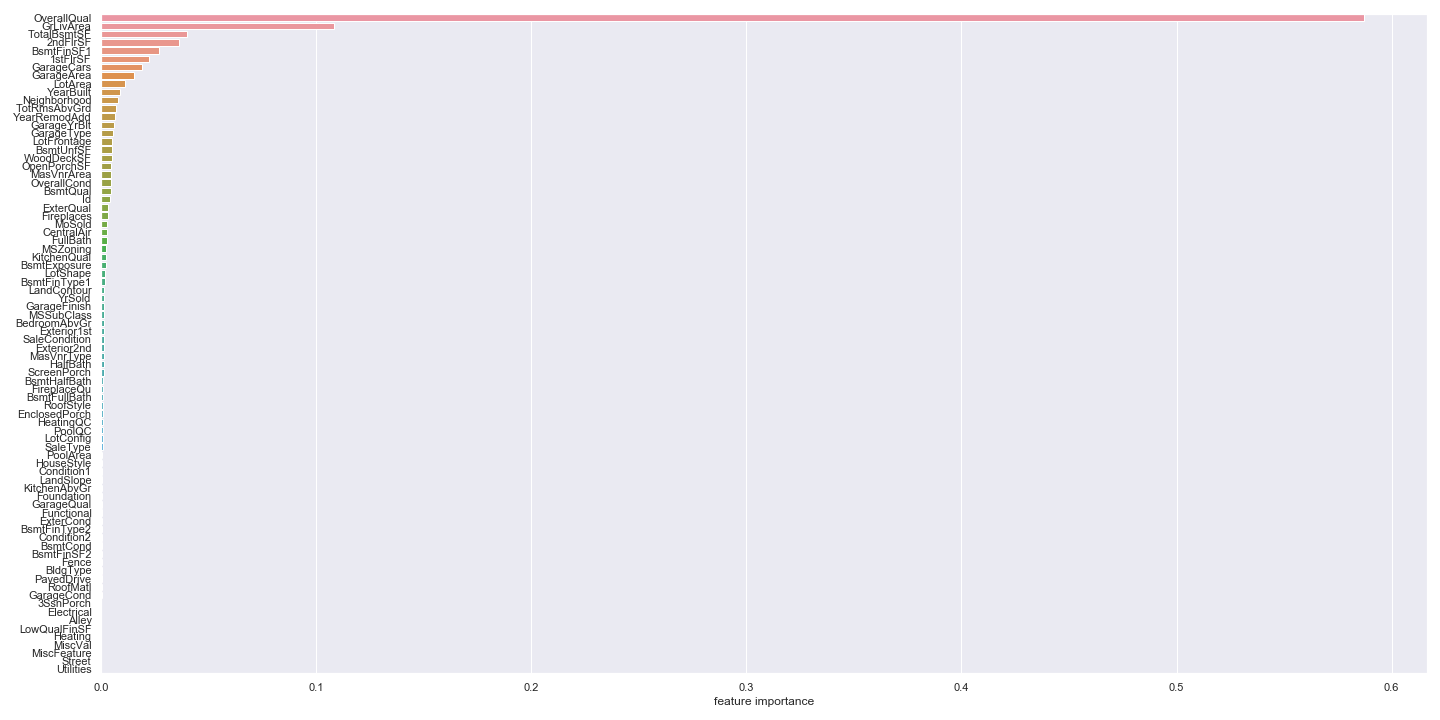
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
y_train = df['SalePrice'] X_train = df.drop(['SalePrice'], axis=1) import matplotlib.pyplot as plt import numpy as np from sklearn.ensemble import RandomForestRegressor import seaborn as sns rf = RandomForestRegressor() rf.fit(X_train, y_train) ranking = np.argsort(-rf.feature_importances_) fig, ax = plt.subplots(figsize=(20, 10)) sns.set() sns.barplot(x=rf.feature_importances_[ranking], y=X_train.columns.values[ranking], orient='h') ax.set_xlabel("feature importance") plt.tight_layout() plt.show() fig.savefig("figure2.png") |
70以上あるFeatureの中で、SalePriceの予測に大切なのはほんの数個しかない、ということがわかります。
[EDA] 散布図や箱ひげ図を用いた目的変数と、説明変数の関係の可視化
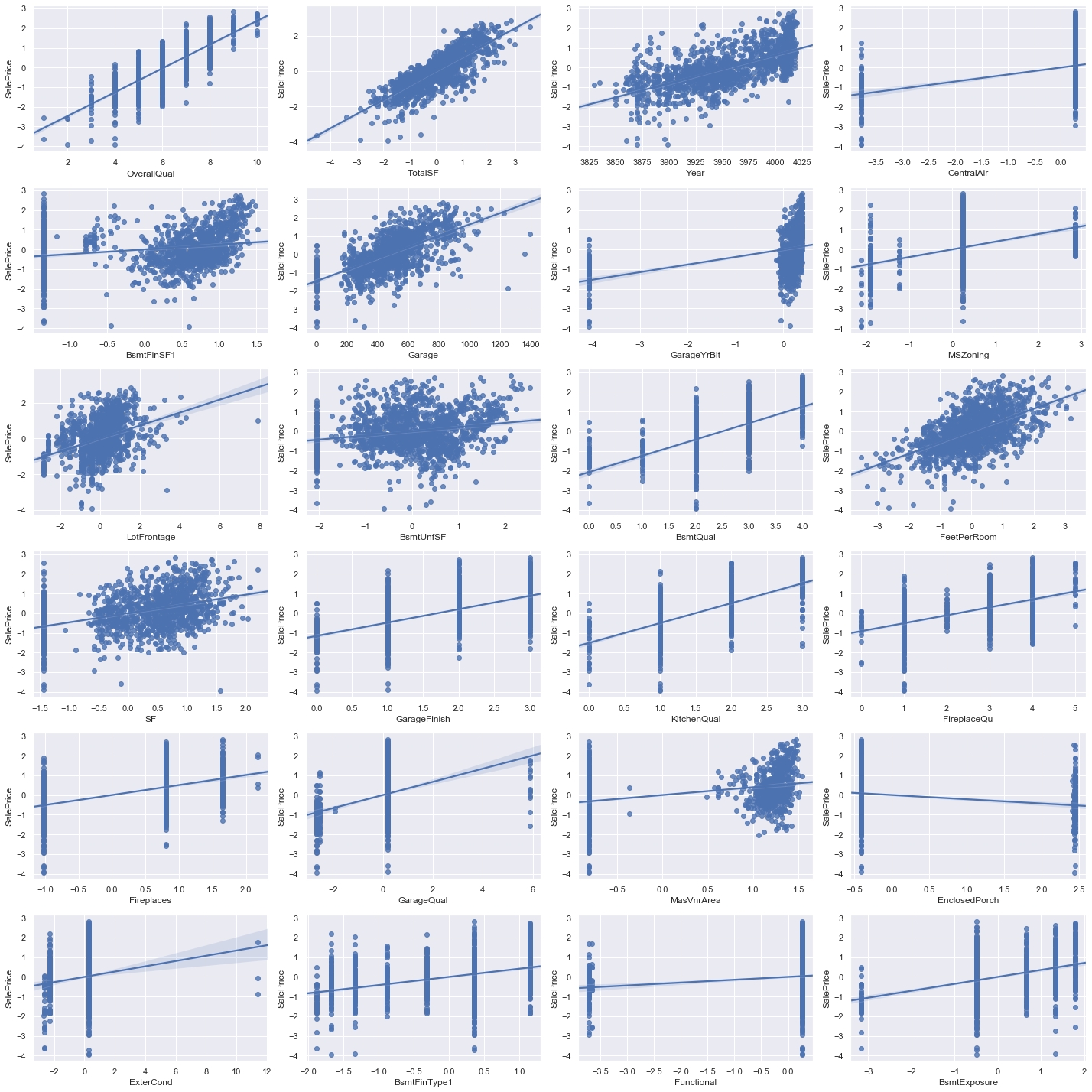
vs SalePriceの上位24変数をプロットしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# relation to the target fig = plt.figure(figsize=(20,20)) ranking = np.argsort(-rf.feature_importances_) X_train = df.drop(['SalePrice'], axis=1) X_train = X_train.iloc[:,ranking[:24]] for i in np.arange(24): # fig.add_subplot(行,列,場所) ax = fig.add_subplot(6,4,i+1) sns.regplot(x=X_train.iloc[:,i], y=y_train) plt.tight_layout() plt.show() fig.savefig("figure3.png") |
線形の関係性が読み取れるものが幾つかあります。
外れ値 (outlier)を再度除去したい場合には、手順を戻って「除去→欠損値の補完」を繰り返します。
学習データとテストデータを統合
最後に学習データとテストデータを統合します。
|
1 2 3 4 5 |
#学習データとテストデータを統合 all_data = pd.concat([X_train, X_test], axis=0, sort=True) #データのサイズを確認 print("all_data: "+str(all_data.shape)) |
マージされた「all_data」というリストが作成されました。
|
1 |
all_data: (2906, 49) |
次回は、これを使って学習モデルを形成します。
ソースコード
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 |
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.ensemble import RandomForestRegressor from sklearn.preprocessing import LabelEncoder from sklearn.preprocessing import PowerTransformer DEBUG = False # 外れ値の削除 def del_outlier(df): df = df.drop(df[(df["TotalSF"]>10000) & (df["SalePrice"]<300000)].index) for col in df: if df[col].dtype != "object" and col != "SalePrice": df = df.drop(df[(df[col]>=0) & (df["SalePrice"]>600000)].index) df = df.drop(df[(df["OverallQual"]<10) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["OverallQual"]<5) & (df["SalePrice"]>200000)].index) df = df.drop(df[(df["SF"]>=0) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["Garage"]>=0) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["Year"]>=0) & (df["SalePrice"]>500000)].index) df = df.drop(df[(df["Year"]<3900) & (df["SalePrice"]>400000)].index) return df # 多重共線性の削除 def del_multicollinearity(df): df["Garage"] = df["GarageCars"] + df["GarageArea"] df["Year"] = df["YearBuilt"] + df["YearRemodAdd"] df["SF"] = df["WoodDeckSF"] + df["OpenPorchSF"] df["TotalSF"] = df["1stFlrSF"] + df["2ndFlrSF"] + df["TotalBsmtSF"] + df["GrLivArea"] # カラム削除 cols = ["GarageCars","GarageArea","1stFlrSF", "2ndFlrSF", "TotalBsmtSF", "GrLivArea", "YearBuilt", "YearRemodAdd", "WoodDeckSF", "OpenPorchSF"] for i in cols: df = df.drop(i, axis=1) return df # 欠損値補完 def do_imputation(df): df['LotFrontage'] = df.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median())) for col in df: #check if it is a number if df[col].dtype != "object": df[col].fillna(0.0, inplace=True) else: df[col].fillna("NA", inplace=True) return df # 順序関係に従ってエンコーディング def encode_mapping(df, i): num=-1 mapping={} for j in df.groupby(i)['SalePrice'].mean().sort_values().index: num+=1 mapping[j]=num df[i]= df[i].map(mapping) return df def encode_categorical1(df): cols = ("MSZoning", 'FireplaceQu', 'BsmtQual', 'BsmtCond', 'GarageQual', 'GarageCond', 'ExterQual', 'ExterCond','HeatingQC', 'PoolQC', 'KitchenQual', 'BsmtFinType1', 'BsmtFinType2', 'Functional', 'Fence', 'BsmtExposure', 'GarageFinish', 'LandSlope', 'LotShape', 'PavedDrive', 'Street', 'Alley', 'CentralAir') for col in cols: df = encode_mapping(df, col) return df # ラベルエンコーダー def encode_label(df, i): lbl = LabelEncoder() lbl.fit(list(df[i].values)) df[i] = lbl.transform(list(df[i].values)) return df def encode_categorical2(df): cols = ("MSZoning", 'FireplaceQu', 'BsmtQual', 'BsmtCond', 'GarageQual', 'GarageCond', 'ExterQual', 'ExterCond','HeatingQC', 'PoolQC', 'KitchenQual', 'BsmtFinType1', 'BsmtFinType2', 'Functional', 'Fence', 'BsmtExposure', 'GarageFinish', 'LandSlope', 'LotShape', 'PavedDrive', 'Street', 'Alley', 'CentralAir') for col in cols: df = encode_label(df, col) return df # 不要変数の削除 def del_variable(df): cols = ("MSSubClass", "OverallCond", "YrSold", "MoSold", "Id", "LandContour", "Utilities", "LotConfig", "Neighborhood", "Condition1","Condition2", "BldgType", "HouseStyle", "RoofStyle", "RoofMatl", "Exterior1st", "Exterior2nd", "MasVnrType", "Foundation", "Heating", "Electrical", "GarageType", "KitchenAbvGr", "MiscFeature", "SaleType", "SaleCondition") for i in cols: df = df.drop(i, axis=1) return df # 歪度の絶対値が0.5より大きい変数だけに絞る def count_skew(df): # 数値の説明変数のリストを作成 num_feats = df.dtypes[df.dtypes != "object"].index # 各説明変数の歪度を計算 skewed_feats = df[num_feats].apply(lambda x: x.skew()).sort_values(ascending = False) # 歪度の絶対値が0.5より大きい変数だけに絞る skewed_feats_over = skewed_feats[abs(skewed_feats) > 0.5].index if (DEBUG): # 各変数の最小値を表示 for i in skewed_feats_over: print(str(min(df[i])) + "\t" + str(i)) return skewed_feats, skewed_feats_over # Yeo-Johnson変換 def trans_yeo_johnson(df, skewed_feats_over): pt = PowerTransformer() pt.fit(df[skewed_feats_over]) # 変換後のデータで各列を置換 df[skewed_feats_over] = pt.transform(df[skewed_feats_over]) # 各説明変数の歪度を計算 skewed_feats_fixed = df[skewed_feats_over].apply(lambda x: x.skew()).sort_values(ascending = False) return df # 新たな特徴量の追加 def add_new_feature(df): # 特徴量に1部屋あたりの面積を追加 df["FeetPerRoom"] = df["TotalSF"]/df["TotRmsAbvGrd"] return df # [EDA]ランダムフォレスト def do_RandomForestRegressor(df): y_train = df['SalePrice'] X_train = df.drop(['SalePrice'], axis=1) rf = RandomForestRegressor() rf.fit(X_train, y_train) return rf # [EDA]説明変数の関係の可視化 def visualize_target(df, rf): fig = plt.figure(figsize=(20,20)) ranking = np.argsort(-rf.feature_importances_) y_train = df['SalePrice'] X_train = df.drop(['SalePrice'], axis=1) X_train = X_train.iloc[:,ranking[:24]] for i in np.arange(24): # fig.add_subplot(行,列,場所) ax = fig.add_subplot(6,4,i+1) sns.regplot(x=X_train.iloc[:,i], y=y_train) plt.tight_layout() plt.show() fig.savefig("figure3.png") def main(df_train, df_test): # 学習データ df_train = del_multicollinearity(df_train) df_train = del_outlier(df_train) df_train = do_imputation(df_train) df_train = del_variable(df_train) df_train = encode_categorical1(df_train) df_train = add_new_feature(df_train) skewed_feats, skewed_feats_over = count_skew(df_train) df_train = trans_yeo_johnson(df_train, skewed_feats_over) rf = do_RandomForestRegressor(df_train) visualize_target(df_train, rf) #----------------------------------------- # テストデータ df_test = del_multicollinearity(df_test) df_test = do_imputation(df_test) df_test = del_variable(df_test) df_test = encode_categorical2(df_test) df_test = add_new_feature(df_test) skewed_feats, skewed_feats_over = count_skew(df_test) skewed_feats_fixed = trans_yeo_johnson(df_test, skewed_feats_over) #学習データを目的変数とそれ以外に分ける X_train = df_train.drop("SalePrice", axis=1) X_test = df_test y_train = df_train["SalePrice"] # 学習データとテストデータを統合 all_data = pd.concat([X_train, X_test], axis=0, sort=True) print("all_data: "+str(all_data.shape)) # CSV読み込み sns.set() df_train = pd.read_csv("train.csv") df_test = pd.read_csv("test.csv") main(df_train, df_test) |
まとめ
前回、方針を決めたにも関わらず、学習データを用意するのに、こんなに苦労するとは思いませんでした。
更に多くのライブラリやlambda(無名関数)式のような記載方法があるため学習が必要です。
しかし、機械学習を始めるまでが本当に長い・・・。