2009年12月24日(木) 来年は女性と過ごしたい
男2人で、クリスマスイブにGALA湯沢(新潟)でスノーボード!!
去年は体調不良で行けなかったので、24日スノボは2回目です。

濃霧です
10m先が見えません(昼からは快適)
24日は人が少なく、クリスマスソングがゲレンデに流れており素敵です。
ただ、
私は寒いのが苦手です
私はスノーボードが好きじゃないです
もう、なんだか義務感でやってます・・・・
2009年12月22日(火) お見合いの理論 by 鳩山由紀夫氏
鳩山由紀夫氏が専修大学で助教授をしていたときに寄稿した論文に「見合いの数理」というものがあります。
概要は以下のようなものです。
「一番すばらしい女性と結婚したいなと。それをどうやったらうまくいくのか」
だったようです。
命題「10人の女性と順番にお見合いする。
その中で一番すばらしい人にプロポーズする確率を最大にしたい。どうしたらいいか」
実際に解いてみましょう。3人の女性(n=3)とお見合いをするとします。
条件を簡単にするために次のように定めます。
- 男性が女性に対してのみプロポーズする
- 「女性が断る」ことは無い
- プロポーズしたら結婚できる
- 一度断ったら復活折衝はない
- 女性の優劣(素晴らしいor not)は決まっている(素晴らしい順に 1, 2, 3 とおく)
表 n=3 の場合
| 女性の登場順序 | 何人目以降でプロポーズした場合に「1」と結婚できるか s – 1 | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| 1 2 3 | o | ||
| 1 3 2 | o | ||
| 2 1 3 | o | ||
| 2 3 1 | o | o | |
| 3 1 2 | o | ||
| 3 2 1 | o | ||
| 1と結婚できる確率 | 33%(2/6) | 50%(3/6) | 33%(2/6) |
女性は素晴らしい順に番号(1番,2番,3番・・)がついているとします。
このとき、人生で3人の女性出会うとしたら出会い方は全6通りです。
またs-1=1では、1人目は無条件に見送り、
2人目以降はその前に現れた人よりも素晴らしい女性であれば、その人にプロポーズします。
s-1=2では、無条件にプロポーズします。
これを計算式にすると次のようになります。
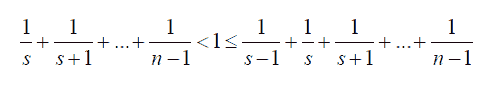
nはプロポーズする総数、(s-1)は一番すばらしい人にプロポーズする順序
要は、人生で3人の女性に出会う場合には1人目は見送るのが良いという結果です。
2009年12月21日(月) パソコン故障2回目
Dellのパソコンが、また故障しました。
電源が入りません。
年末に実家に持ち帰る予定でしたが、どうしようもありません。
残念だよね。