「データサイエンティストのためのスキルチェック」は幅広い知識が試される

Excelでデータ集計して分析、課題発見するのが私の仕事の一つ。

今流行のデータサイエンティストと呼ぶにはおこがましい旧式タイプだと思ってるけどね。

そんなある日……

あー君、君、分析が仕事だよね？
ちょっと、これ受けておいてよ。アンケートらしいから。

部長の命令は「ウンコ食え」と言われても従います。
了解しました！

あーそう？ちょうど今から糞行こうと思ってたけど食う？

……。

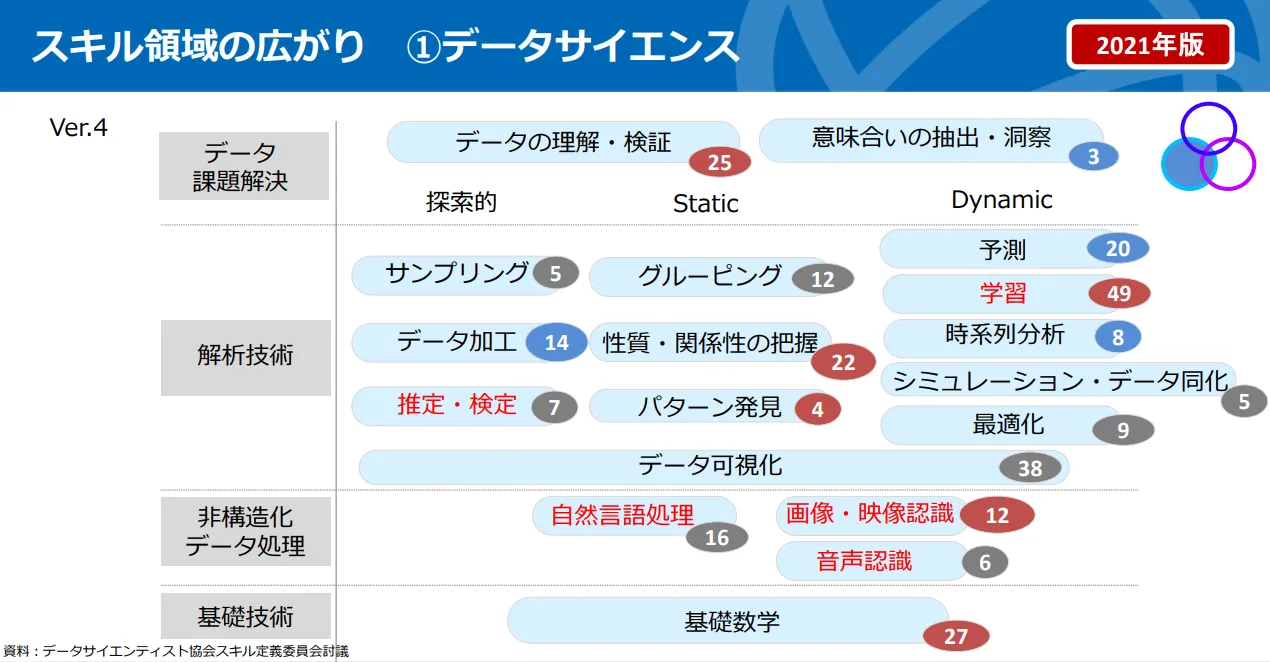
クソみたいな会話した後に、URLに飛ぶと「データサイエンティストのためのスキルチェックリスト/タスクリスト概説」のページが開いた。

これ知ってるよ……

一般社団法人データサイエンティスト協会は、独⽴⾏政法⼈情報処理推進機構（以下、IPA）が共同で刊⾏したものだ。

既に簡単に中身は確認済みで、内容が統計学、機械学習、クラウド……と幅広かったような。

使うべき局面と適切な使い方
統計学的な知識
機械学習的な知識アンケート
おわりに

案の定、半分以上よく分からない世界で撃沈……

後学のために抜粋して書き残しておく。

使うべき局面と適切な使い方

代表値（平均値・中央値・最頻値）、散らばりの尺度（分散・標準偏差・絶対平均偏差等）、相関係数を用いて、データを理解することができる

初っ端から躓いた……。

平均とか分散、相関係数は知ってる。過去の日記でも何度も書いてる。

「平均・分散」の計算を、計算コストを減らして短いソースコードで書く

中間発表が終了。ネットワークが落ちたりと…あまり進んでいませんが…家のADSLも不安定だし…研究は数式ばかりでよく分かりません。ただ、式を分解して最適に変換することでプログラム作成にとって非常に楽になる事が分かりましたの...

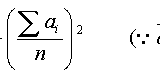
でも「絶対平均偏差値」って何だっけ？

ネット見ても「一般的にばらつきの指標は標準偏差が利用されます。平均偏差は使われるのを見たことがありません。」と書いてあるけど。

平均絶対偏差

各データに対して「平均値との差」（＝偏差）の絶対値を計算し、その総和をデータ数で割った値（＝平均値）を表す

あーそうそう、カンニングしちゃ駄目よ？

……。

カンニングしたくなるアンケートって何やねん。

ヒストグラム・棒グラフ・散布図・箱ひげ図・ヒートマップについて、使うべき局面と適切な使い方を説明することができる

こんな事も、意識してないよ。

いろいろなグラフに当てはめてみて考察に適していると使うんじゃないの？

種類	意味	例
絵グラフ	同形の絵を並べ、量の大小を比較する。
棒グラフ	棒の高さで、量の大小を比較する。
折れ線グラフ	量が増えているか減っているか、変化の方向をみる。
円グラフ	全体の中での構成比をみる。
帯グラフ	構成比を比較する
ヒストグラム	データの散らばり具合をみる。
箱ひげ図	データの散らばり具合をみる
ヒートマップ	のデータを、色の濃淡でわかりやすく表現したもの
散布図	2つの量に関係があるかどうかをみる

この辺りまではノリノリだったが……

ここからExcelでピボットテーブル使って分析している時に全く必要ない知識のオンパレード……

統計学的な知識

因みに、これ高校生が「情報I（統計学）」で学ぶ範囲。

大学でも学んだ記憶ないなぁ……。

精度評価指標

以下の精度評価指標について、その意味と使い方を説明することができる
# 決定係数、RMSE、AUC（Area Under Curve）、正解率／適合率／再現率／F値

AUC（Area Under Curve）は知ってるが、後は知らん。

機械学習で株価予測（交差検証＋ROC 曲線とAUCで精度65%）

日本では5つの要因でサラリーマンの給料は上りません。① 労働組合の弱体化② 非正規雇用者の増加③ 少子高齢化の影響④ 内部留保を貯め込んで賃金を上げない経営者⑤ 規制緩和の遅れがもたらした賃金低迷この...

指標	意味
決定係数	回帰分析によって求められた目的変数の予測値が、実際の目的変数の値とどのくらい一致しているかを表している指標
RMSE	二乗平均平方根誤差(RMSE) とは、MSEに平方根をとることで計算されるもの
AUC	ROC曲線を作成した時に、グラフの曲線より下の部分の面積
正解率	予測結果全体がどれくらい真の値と一致しているかを表す指標
適合率	正事例と予測したもののなかで真の値が正事例の割合を表す指標
再現率	真の値が正事例のもののなかで正事例と予測した割合を表す指標
F値	説明分散／非説明分散で計算され、大きければ大きい程、その回帰モデルは信頼できることを示す

RMSEは二乗平均平方根誤差のことか……

統計的仮説検定

統計的仮説検定において、帰無仮説と対立仮説、第1種の過誤、第2種の過誤、p値、有意水準、片側検定と両側検定の意味を説明できる

検定	意味
帰無仮説	仮説検定で捨てるか捨てないか決めようとする仮説
対立仮説	その当否が検定される帰無仮説に対立する仮説
第1種の過誤	本当は差がないのに「差がある」と判定してしまうこと
第2種の過誤	帰無仮説が正しくないのに関わらず（真でないのに）、真として棄却しない誤りのこと
p値	帰無仮説の元で検定統計量がその値となる確率のこと
有意水準	帰無仮説が間違っていると判断する（帰無仮説を棄却する）基準となる確率のこと
片側検定	帰無仮説を立てたときに棄却域を確率分布の片側だけに設定する検定
両側検定	帰無仮説を立てたときに棄却域を確率分布の両側に設定する検定

検定する対象となるデータの対応の有無を考慮した上で適切な検定手法（t検定, z検定など）を選択し、適用できる

検定手法	意味
t検定	条件の異なる2つの群において、それぞれの群の平均値の間の差が統計的に有意なものなのか、それとも偶然なのかを判定する手法
z検定	母集団の平均と標準偏差が判明している場合に、与えられた数値が母集団と一致しているかを判定する手法（母集団の標準偏差が分かっていることは稀なので、あまり使わない）

今では何でもYouTubeで学べる時代。

【情報Ⅰ共通テスト】母集団と標本／仮説検定（Z検定とｔ検定）／帰無仮説・有意水準、自由度、ｔ分布、両側検定・片側検定について解説／統計学

適切な検定手法

検定力やサンプルサイズ、分布など対象のデータを考慮したうえで適切な検定手法を選択し、結果を評価できる（パラメトリックな多群の検定、クラスカル・ウォリス検定、カイ二乗検定など）

検定手法	意味
パラメトリックな多群の検定	母集団分布が正規分布であることを仮定した上でそれぞれの母平均の比較をおこなう方法
ノンパラメトリックな多群の検定	各群ごとの母集団分布について必ずしも正規分布を想定しない状況で比較をおこなう方法
クラスカル・ウォリス検定	3群以上の独立したサンプルの比較を行うノンパラメトリック検定の手法
カイ二乗検定	帰無仮説が正しければ検定統計量が漸近的にカイ二乗分布に従うような統計的検定法

分析の対象を定める段階で選択バイアスが生じる可能性があることを理解している（途中離脱者の除外時、欠損データの除外時など）

選択バイアス

観察するサンプリング（抽出）された集団が、全体の様子を反映していない偏りのこと

欠損データの除外は何度かブログで紹介したが、それによるバイアスの考慮は一切していない。

KaggleのHouse Pricesで回帰分析（Feature Engineering編）

今回も、kaggleの入門者向けチュートリアルコンペ「住宅価格予測」を解いてみます。House Prices: Advanced Regression Techniques各種指標を用いて住宅の価格を予測する分析...

ある変数の影響（因果効果）を推定したいがランダム化比較試験の実施が難しい場合、傾向スコアによる手法（傾向スコアマッチング、IPW、Doubly Robustなど）を用いることで観測されている共変量の影響を最小限に抑えることができる

傾向スコアによる手法	意味
傾向スコアマッチング	類似した傾向スコアをもつ対象者同士をマッチングして，解析用データを作る方法
IPW	逆数重み推定(IPW)。各対象者のデータを傾向スコアの逆数で重みづけしてあげることで、より疑似母集団を作成して重みづけ平均をとる手法
Doubly Robust	二重にロバスト（DR：Doubly Robust）な推定法。IPW推定量よりも漸近分散が小さい

機械学習的な知識アンケート

このあたりの知識は何度もブログでも紹介しているので割愛。

適切なデータ区間設定でヒストグラムを作成し、データのバラつき方を把握できる
適切な軸設定でクロス集計表を作成し、属性間のデータの偏りを把握できる
量的変数の散布図を描き、2変数の関係性を把握できる
縦軸や横軸以外の要素（色や形状）に変数をマッピングしたり、チャートの層別（Facet）をすることによって、カテゴリ間の傾向の違いを把握することができる
高次元のデータを主成分分析などで低次元データに変換した上で、チャート（散布図など）で表現することができる
自らが設定した問いの解を探すように可視化するプロセスを繰り返すことで、ビジネス／データの理解を連鎖的に深め／広げることができる（EDA：探索的可視化）
データの可視化を通じて仮説設定・検証を行い、ストーリーとして組み立て伝えることができる
探索的可視化を通じて得られたインサイトを、モデル生成時の特徴量のアイディアとして活用することができる

ホールドアウト法、交差検証（クロスバリデーション）法の仕組みを理解し、学習データ、パラメータチューニング用の検証データ、テストデータを作成できる

手法	意味
ホールドアウト法	モデル構築用の答えが分かっているデータを予め「構築用」と「検証用」の2つに分けてからモデルを作成する方法
クロスバリデーション法	データ十分数ない時でも有効、K分割交差検証法。既存データをK個に分割し、K-1個のデータでモデルを作り、構築に使用したK-1個のデータと、未使用の1個のデータを予測させてその精度差を測る方法

クロスバリデーション（cross-validation）は何度かブログで紹介した。

KaggleのHome Credit Default Risk体験（他人のKernelパクリ編）

過去の「Featured」として、まずはタイタニック同様の「分類」コンテストで有名な次の問題を解いてみます。Home Credit Default Riskこのコンペは与えられた個人のクレジットの情報や以前の応募...

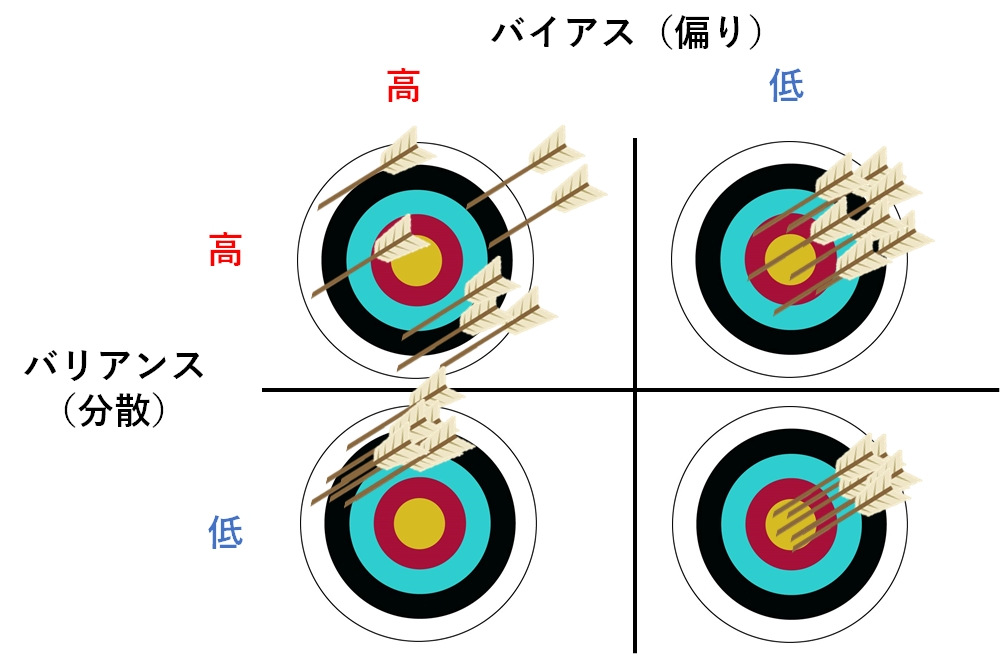
バイアス・バリアンスのトレードオフ

バイアス（偏り：Bias）とは、予測値と真の値（＝正解値）とのズレ（つまり「偏り誤差：Bias error」）を指す。

バリアンス（分散：Variance）とは、予測値の広がり（つまり「ばらつき誤差：Variance error」）を指す。

この辺は何度かブログでも紹介した。

KaggleのHouse Pricesで回帰分析（モデル作成編）

特徴量化

知っているものもあるし、記憶が曖昧なものもある。

数値データの特徴量化（二値化／離散化、対数変換、スケーリング／正規化、交互作用特徴量の作成など）を行うことができる

特徴量化	意味
二値化／離散化	ターゲットの値を二値にする処理／ある連続した値を不連続な値に分割する処理
対数変換	データに対して対数（Log）をとること
スケーリング／正規化	データをある基準に沿って変換し尺度を統一すること／特徴量の値の範囲を一定の範囲におさめる変換
交互作用特徴量	二つ以上の変数をかけ合わせた新しい変数を作る方法のこと

カテゴリデータの特徴量化ができる（ダミー変数化、特徴量ハッシング[カテゴリ数が多い場合の値の割り当て]、ビンカウンティング、バックオフ、最小カウントスケッチ[レアなカテゴリのまとめ処理]など）

特徴量化	意味
ダミー変数化	カテゴリ変数を数字に変換する手法。数字ではないデータを「0」と「1」だけの数列に変換する手法
特徴量ハッシング	任意の特徴をベクトルあるいは行列のインデックスに変換する手法
ビンカウンティング	カテゴリ値ごとに別の集計値に置き換える手法
バックオフ	群をまとめて一つのカテゴリとして扱う単純な方法
最小カウントスケッチ	最小(min)の値を要素が追加された数として返す手法

重回帰モデルの解釈に必要な統計的手続きの知識を有しており（変数選択、多重共線性、残差の正規性、有意性など）、ライブラリを使って重回帰モデルの生成し、回帰係数を適切に解釈することができる

特徴量化	意味
変数選択	モデルに入る変数を選ぶ作業
多重共線性	説明変数の中に、相関係数が高い組み合わせが存在すること
残差の正規性	残差平方和やカイ2乗検定の事後検定としての残差分があるデータが正規分布に従っていること
有意性	データに示される因果関係、一致又は不一致の関係、相関又は逆相関の関係等が、確率的に偶然とは考えがたく意味を持つと推定されること

オッズ比を使って、ロジスティック回帰モデルの回帰係数の解釈をすることができる

特徴量化	意味
オッズ比	ある事象の起こりやすさを2つの群で比較して示す統計学的な尺度
回帰係数	回帰分析において、座標平面上で回帰式で表される直線の傾き

次元の呪いの影響を受けやすいアルゴリズムを識別し対処するアプローチを知っている（特徴量選択、次元圧縮、L1/L2正則化など）

特徴量化	意味
特徴量選択	機械学習のモデルを使用する際に有効な特徴量の組み合わせを探索するプロセスのこと
次元圧縮	多次元からなる情報を、その意味を保ったまま、それより少ない次元の情報に落とし込むこと
L1/L2正則化	余分な説明変数を省くことを目的とした手法

LIME、SHAPなどを用いて、ブラックボックス性の高いモデルの局所的な説明（レコード単位の予測根拠の提示）ができる

これは、AIの判定根拠を示す「説明可能AI」のことだ。

特徴量化	意味
LIME	あるデータに対するAIモデルの予測について、寄与した特徴量とそのスコアを可視化する技術
SHAP	説明したいインスタンスの予測値と、全てのインスタンスの平均との間の差分を、各特徴量ごとの貢献度に分配する手法

時系列データ分析

時系列分析を行う際にもつべき視点を理解している（長期トレンド、季節成分、周期性、ノイズ、定常性など）

時系列データとは、時間の順序にしたがって並べられたデータのことをいう。

時系列データには大きく分けて「傾向変動」「季節変動」「循環変動」「不規則変動」の4つの情報（要因）を持っている。

また、時系列データにおける重要な概念として「定常性」「単位根過程」「自己共分散」の3つある。

特徴量化	意味
長期トレンド	時間の経過とともに増加・減少する傾向。推定方法には「移動平均」など
季節成分	（通常）1年を周期とする規則的な変動のこと
周期性	時系列が⼀定の間隔で同じような変動を繰り返す成分、またはその状態
不規則変動（ノイズ）	トレンド、季節変動、循環変動では説明できない、短期的かつ不規則な変動のこと
定常性	時間経過による影響を（強く）受けない状態

時系列データに対し、ライブラリを使用して、分析結果の比較を行い、適切なモデルを選択できる（自己回帰モデル[AR]、移動平均モデル[MA]、ARIMA、SARIMA、VAR、GARCH、Prophet、指数平滑法など）

特徴量化	意味
自己回帰モデル	現在の値を過去のデータを用いて回帰するモデル。失業率といった経済指標、株価の分析などに用いる
移動平均モデル	現在・過去のホワイトノイズ線形和に定数を加えて単変量の現在値を表現するモデル
ARIMA	自己回帰和分移動平均モデル
SARIMA	ARIMAモデルに「季節的な周期パターン」を加えたモデル
VAR	ベクトル自己回帰(VAR)モデル。自己回帰(AR)モデルを多変量に拡張したもの
GARCH	ARCHモデルをより一般化したモデル。より長くデータのブレが広がる状況が持続するモデルを少ないパラメータで表現する手法
Prophet	Meta が公開している時系列解析向けのライブラリ
指数平滑法	過去の予測値と実績値を割り出し、両方を使って需要を予測する手法