東京証券取引所では、1年の最後の取引日である「大納会」が12月30日、1年の最初の取引日である「大発会」が1月4日。
これを利用したイベント投資に関する記事が昨年の年末に公開されていた。
年内の最終日の12月30日にに連動する商品を買って年始の1月4日に売るのも勝率が高くなります。
年末年始は長い休日になるため、何が起きるかわかりません。リスクを回避するために保有している株式をいったん売却して、年が明けてから買い直す投資家が多いことが影響していると思います。
｢12月30日に買って1月4日に売るだけ｣30代で1億円つくった人が本当は教えたくない"ある投資手法" | PRESIDENT WOMAN Online（プレジデント ウーマン オンライン）
※本稿は、まつのすけ『33歳で1億円達成した僕が実践する一生モノの億超え投資法』（KADOKAWA）の一部を再編集したものです。イベント投資は定期的に起こる出来事に対して、今後も同じことが起きると考えて投資を…
president.jp
これ本当なのかな？
ググれば色々な似た記事があるけど、バックテストしてみたら良いんじゃない？
【投資の着眼点】検証してみた！ 「年末年始は株価が上がりやすい」はホントか？
2019年も残すところ、あと1か月である。今年の株式市場を振り返ってみると、日経平均株価は年初から4月にかけては前年の10月から12月にかけての世界的な株価急落に見舞われた後の反発もあって、堅調に推移していた。しかし、5月から本格化した米中関税戦争、6月から始まった香港民主化デモなどの影響を受けて、今夏の株価は不安定な...
www.j-cast.com
年末年始でボケた脳みそをフル回転できるように、数式交じりになっている。
「12月30日に買って1月4日に売る」期待値検証
説明を読んで次のように定義した。
【基本条件】
- 1) 初期費用 300万円
- 2) 単利運用
- 3) 現物取引：1銘柄当たり仕掛け金額50万円
- 4) 買い
- 5) 売買対象：日経平均株価に連動する銘柄
- 6) 終値が100円以上
- 7) 20日平均売買代金 20億以上
【買い条件】
- 1) 大納会（12月30日）の終値で買い
【売り条件】
- 1) 大発会（1月4日）の始値で売り
【仕掛けの優先順位】
- 1) 5日移動平均線乖離率 昇順
「日経平均株価に連動する銘柄」はググったところ「36か月β値（ベータ値）」というもので求めるのが一般的のようだ。
対日経平均β値（ベータ）とは何か？
対日経平均β値とは、日経平均株価が一定割合で動いたときに、その何倍動くかを表す数値。
過去の取引日において、当該銘柄の値動きが日経平均の値動きと、どの程度連動していたかを表す指標として利用される。
○○銘柄のβ値 = ○○銘柄株式のリターンと日経平均株価のリターンの共分散 ÷ 日経平均株価のリターンの分散
ある銘柄の対日経平均ベータ（36ヶ月）が1.2だとすると、平均的には日経平均が10%上昇したときには12%上昇し、日経平均が10%下落したときには12%下落する傾向があることを意味しています。
つまり、ベータが1の株式の株価は、株式市場と同じように変動するため、株式市場（インデックス）の期待リターンと同じだけ、その株式に投資するとリターンが期待できると考える。
例として、JR東海とTOPIXの月次のリターンを計算する。
※ リターン = 当月の株価 / 前月の株価 – 1
企業価値評価におけるベータ（β）値の計算例 | 上原FAS合同会社
初心者の方が割引率を計算する際に一番悩む論点、それがベータだと思います。ベータはTOPIXなどのインデックスと個別の株式のリターンの相関性を表す指標であり、エクセルを用いれば誰でも計算できます。とはいえ、なんとなく計算できたとしても本当にあ
roadtoartisan.com
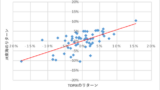
ExcelならLINEST関数を使うらしい。
LINEST 関数は、”最小二乗法” を使って「係数（直線の傾き）」と「定数項（切片）」を求めている。
最小二乗法（一次関数）の係数を決定する手順
はい、みんな大好きな数学の時間。
最小二乗法は近似式との差の二乗の総和が最小になる近似式を求めること。
近似式である直線の方程式が 
と表されるとすると、データ点との二乗の差の総和
は次のようになる。
![\[S(a, b)= \sum\limits_{ i = 1 }^{ N }\{y_i - (ax_i + b)\}^2\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-cc6f8d098516b7d1b0b2619345a558a6_l3.png "Rendered by QuickLaTeX.com")
解き方は色々ある。
主成分分析が固有値問題となる理由
行列には「固有値」や「固有ベクトル」、統計には「分散」や「共分散」があるというのは、理系の大卒なら誰でも知っている。しかし、数学として固有方程式を解く方法だけ学んでも、結局何のためにあるのかわからないまま終わってしまう。...
nehori.com
2019.04.22
直感的なのは が極小を取るようにするために、
と
の各々で偏微分してどちらも
にする方法だ。
![\[\frac{\partial S (a, b)}{\partial a} = 2 \sum\limits_{i=1}^{N} x_i (ax_i + b - y_i) = 2 \sum\limits_{i=1}^{N} (a x_i^2 + b x_i - x_i y_i) = 0\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-9dd699bb0bb8da84c558cad467c0afe9_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{\partial S (a, b)}{\partial b} = 2 \sum\limits_{i=1}^{N} (a x_i + b - y_i) = 0\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-4d602bf4c6f302d8a5e521e3fbe2c40b_l3.png "Rendered by QuickLaTeX.com")
これらより、次の連立方程式が得られる。
![\[a \sum\limits_{i=1}^{N} x^2_i + b \sum\limits_{i=1}^{N} x_i = \sum\limits_{i=1}^{N} x_i y_i\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-3250a0b0de94538ab5c86f443d3af43d_l3.png "Rendered by QuickLaTeX.com")
![\[a \sum\limits_{i=1}^{N} x_i + N b = \sum\limits_{i=1}^{N} y_i\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-170a4806ba0b67994768b4b159ca480b_l3.png "Rendered by QuickLaTeX.com")
は測定データ数で、上の 2 式より、 と を決定できる。
![\[a = \frac{ N \sum\limits_{i=1}^{N}x_i y_i - \sum\limits_{i=1}^{N} x_i \sum\limits_{i=1}^{N}y_i }{N \sum\limits_{ i = 1 }^{N} x^2_i - (\sum\limits_{ i = 1 }^{N} x_i)^2}\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-51d9ccada9f949849613c2ad6d8ea341_l3.png "Rendered by QuickLaTeX.com")
![\[b = \frac{ \sum\limits_{i=1}^{N}x_i^2 \sum\limits_{i=1}^{N}y_i - \sum\limits_{i=1}^{N} x_i \sum\limits_{i=1}^{N} x_i y_i }{N \sum\limits_{ i = 1 }^{N} x^2_i - (\sum\limits_{ i = 1 }^{N} x_i)^2}\]](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-51ffec29f0be5e01309378947741f76f_l3.png "Rendered by QuickLaTeX.com")
その他、解法には「直接解法 (Direct Method)」と「反復解法 (Iterative Method)」の2つの方法が存在する。
| 解法 | 具体的な解法 |
|---|---|
| 直接解法 | Gauss-Jordan法、Gauss消去法、LU分解、QR分解、特異値分解 |
| 反復解法 | ヤコビ法、ガウス・ザイデル法、SOR法、共役勾配法 |
バックテスト結果
バックテスト時間は全銘柄で15分。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
株価データ: 日足 銘柄リスト: 全銘柄 2005/01/04～2022/01/05における成績です。 ---------------------------------------- 全トレード数 92 勝ちトレード数(勝率) 56(60.87%) 負けトレード数(負率) 36(39.13%) 全トレード平均利率 0.28% 勝ちトレード平均利率 1.38% 負けトレード平均損率 -1.43% 勝ちトレード最大利率 4.04% 負けトレード最大損率 -3.01% 全トレード平均期間 7.25 勝ちトレード平均期間 6.77 負けトレード平均期間 8.00 ---------------------------------------- 必要資金 ¥2,819,560 最大ポジション(簿価) ¥2,969,220 最大ポジション(時価) ¥2,978,650 純利益 ¥118,169 勝ちトレード総利益 ¥359,209 負けトレード総損失 -¥241,040 全トレード平均利益 ¥1,284 勝ちトレード平均利益 ¥6,414 負けトレード平均損失 -¥6,696 勝ちトレード最大利益 ¥20,160 負けトレード最大損失 -¥14,100 プロフィットファクター 1.49 最大ドローダウン(簿価) -¥118,180 最大ドローダウン(時価) -¥163,970 ---------------------------------------- 現在進行中のトレード数 0 ---------------------------------------- 平均年利 0.23% 平均年利(直近5年) -0.25% 最大連勝 6回 最大連敗 3回 ---------------------------------------- [年度別レポート] 年度 取引回数 運用損益 年利 勝率 PF 最大DD 2022年 6回 ¥27,939円 0.99% 100.00% ∞倍 0.00% 2021年 6回 ¥12,990円 0.46% 100.00% ∞倍 0.00% 2020年 6回 -¥47,640円 -1.69% 0.00% 0.00倍 -1.71% 2019年 6回 -¥70,540円 -2.50% 0.00% 0.00倍 -2.71% 2018年 6回 ¥42,670円 1.51% 100.00% ∞倍 0.00% 2017年 6回 ¥30,180円 1.07% 100.00% ∞倍 0.00% 2016年 4回 -¥18,800円 -0.67% 0.00% 0.00倍 -1.13% 2015年 7回 -¥17,560円 -0.62% 14.29% 0.05倍 -1.07% 2014年 6回 -¥17,200円 -0.61% 16.67% 0.12倍 -1.20% 2013年 6回 ¥83,040円 2.95% 100.00% ∞倍 0.00% 2012年 3回 ¥13,860円 0.49% 100.00% ∞倍 0.00% 2011年 3回 ¥16,680円 0.59% 100.00% ∞倍 0.00% 2010年 3回 ¥6,730円 0.24% 100.00% ∞倍 0.00% 2009年 5回 ¥72,860円 2.58% 100.00% ∞倍 0.00% 2008年 5回 -¥60,410円 -2.14% 0.00% 0.00倍 -3.01% 2007年 5回 ¥12,260円 0.43% 100.00% ∞倍 0.00% 2006年 5回 ¥36,600円 1.30% 100.00% ∞倍 0.00% 2005年 4回 -¥5,490円 -0.19% 25.00% 0.00倍 -1.17% |
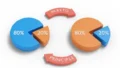
利益曲線は次の通り。
あれ？
想像していたより利益率が低い……。
そして「日経平均株価に連動する銘柄」を選んだので、候補として選ばれた銘柄が次のようなインデックスばかりだった。
- 1306 NEXT FUNDS TOPIX連動型上場投信
- 1348 MAXIS トピックス上場投信
- 1320 ダイワ上場投信－日経225
- 1308 上場インデックスファンドTOPIX
- 1591 NEXT FUNDS JPX日経インデックス400連動型上場投信
- 1329 iシェアーズ・コア 日経225 ETF
……。
何だよこれ！
やる前から分かってたよね……。
年始にやるようなプログラミングじゃねーだろ！！
まとめ
【結論】
｢年内の最終日の12月30日に日経平均株価に連動する商品を買って年始の1月4日に売る｣では、30代で1億円は作れない
© デスノート／大場つぐみ、小畑健／集英社
記事に騙されてバックテストして時間を無駄にしたわ。
分かったことは「最小二乗法の実装は間違っていなかった」だけ……。
こうやって、また一年を無駄にして過ぎていくんだろうな……。
中学校・高校の数学の教員免許の専修過程（校長になれる資格）まで取得した建前、無駄に数学を使うようにしてるけど意味ねーー。
ソースコード
バックテストには無料OSSの「Protra」を利用した。
TIlib、Utility、TrendCheck、TOPIXライブラリはGitHubに置いている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 |
# loop-type: date-only //============================== require "TIlib" require "Utility" require "TrendCheck" // ====================================== // 12月30日に買って1月4日に売る // ====================================== codes = CodeList if ($code_num && $code_num != Length(codes)) Print("前回と異なる銘柄リストでは実行できません。") Dummy end $code_num = Length(codes) //グローバル変数を初期化 if (!$__INIT__) $budgetIni = 3000000 $buyUnit = 500000 // 1回の購入資金 (50万円) $MaxHoldDay = 0 // 最大保有日数 $shortSelling = 0 // 空売り戦略 Yes(1)/No(0) $Interest = 1 // 無制限(0) / 単利(1) / 複利(2) $reverse = 0 // 購入順序 昇順(0) / 降順(1) $udcount = 0 // 騰落レシオ利用数 Init() //------------------------------------------------ $DiffMA = [$code_num] //------------------------------------------------ InitDone() // 騰落レシオ初期化 $__INIT__ = 1 end def CheckDainou() if (Month == 12 && Day == 28 && DayOfWeek == 5) return 1 elsif (Month == 12 && Day == 29 && DayOfWeek == 5) return 1 elsif (Month == 12 && Day == 30) return 1 else return 0 end end // 最小二乗法 def Lsm(x, y, n) xi = (float)0 yi = (float)0 xx = (float)0 xy = (float)0 i = 0 while (i < n) xi = xi + x[i] yi = yi + y[i] xx = xx + x[i] * x[i] xy = xy + x[i] * y[i] i = i + 1 end n = i a = (n * xy - xi * yi) / (n * xx - xi * xi) b = (yi * xx - xi * xy) / (n * xx - xi * xi) return a end // 月次のリターン値 def StockRet(x) retVal = [x] i = 0 while (i < x) if ! ({-1 * i * 20}Close && {(-1 * i - 1) * 20}Close) return end // リターンは当月の株価/前月の株価-1 retVal[i] = (float){-1 * i * 20}Close / (float){(-1 * i - 1) * 20}Close - 1 i = i + 1 end return retVal end def Main(i) //================================================== // 条件(買条件, 売条件共通部分) //================================================== //まだ上場していない銘柄は株価データがないためnullが返る if (Index == null) return end if ($order[(int)Code] == -1) $order[(int)Code] = i end if ! ($DiffMA[i]) // 銘柄ごとのグローバル変数を初期化する $DiffMA[i] = DiffMA_new(5) $hold[i] = 0 return end //指標の計算を1日進める DiffMA_next($DiffMA[i]) //================================================== // 保有してない→購入 //================================================== if (! $hold[i]) diffma = DiffMA_value($DiffMA[i]) if ! (diffma && Close) return end //================================================== // 売買(買い) //================================================== // 1) 大納会 flag1 = CheckDainou() if ! (flag1) return end // 2) 終値が100円以上 flag2 = Close >= 100 if ! (flag2) return end // 3) 20日平均売買代金 20億以上 tv = TradingValume(20) flag3 = tv >= 200000 if ! (flag3) return end // 36か月対日経平均β値が±0.05%の誤差以内 // 当日ギャップ率（騰落率）=（当日終値÷前日終値 - １）×100 x = {Code}StockRet(36) y = {"1001"}StockRet(36) if ! (x && y) return end tmp = Lsm(x, y, 36) flag4 = -0.04 < (tmp - 1) && (tmp - 1) < 0.04 if (flag4) // 当日終値0%で、翌日、指値注文 Print("Code = "+ Code + "/" + tmp) $buyflag[i][0] = Close * 1.00 $buyflag[i][1] = diffma $buyflag[i][2] = 1 $buyCnt = $buyCnt + 1 end //================================================== // 保有している→売却 //================================================== elsif ($hold[i]) if ($set[i] < 1) $set[i] = 1 return end $set[i] = $set[i] + 1 //================================================== // 売買（売り） //================================================== if ($set[i] >= $MaxHoldDay) PrintLog("売り") $sellflag[i] = 1 $set[i] = 0 end end end //================================================== // 買い（当日終値0%で、翌日、指値注文） //================================================== def Buying2(i) if (HasPricedata(Close)) BuyingLimitedPrice(i, 0, Close) end end //==================== // 買い処理 //==================== def SortBuy() if ! (HasPricedata({1}Open)) return end $long = 0 $long = Num($buyUnit, Close) codeset = $order[(int)Code] Buying2(codeset) end //==================== // 売り処理（デイトレ模倣） //==================== def Sell_(i) if (HasPricedata(Open)) if ($sellflag[i]) SellingLimitedPrice(i, 0, {-1}Open) $sellflag[i] = 0 $buyflag[i][2] = 0 end // 使用した$buyflag 配列を初期化 if ($buyflag[i][0]) $buyflag[i][0] = 0 $buyflag[i][1] = 0 end end end //==================== // 銘柄コードを変えながらMain関数,BuySell関数を実行 //==================== Print("-------------------------------------------------") Print("日付 = "+ Year + "/" + Month + "/" + Day) $buyCnt = 0 // 購入数初期化 i = -1 while (i + 1 < $code_num) i = i + 1 {codes[i]}Main(i) end i = 0 if ($buyCnt) sortList = SelectionSort(10, 0) cnt = $buyCnt if ($buyCnt > 10) cnt = 10 end while i < cnt {sortList[i]}SortBuy() i = i + 1 end end //---------------------------------------------- i = -1 while (i + 1 < $code_num) i = i + 1 {codes[i]}Sell_(i) end |
