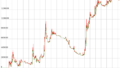
行列には「固有値」や「固有ベクトル」、統計には「分散」や「共分散」があるというのは、理系の大卒なら誰でも知っている。
しかし、数学として固有方程式を解く方法だけ学んでも、結局何のためにあるのかわからないまま終わってしまう。
今回は、そんな話。
※ 色々と式を書き直してましたが「株式会社アイデミー」様のサイトの詳しさに叶わず、ほぼ参考にしてます。
高校・大学の数学復習
分散・共分散・共分散行列
「分散」とは、ある一次元のデータ![]() に対し平均値
に対し平均値![]() からの差の2乗和の平均である。
からの差の2乗和の平均である。
式で書けば次のようになる。
![]()
分散はデータのバラつきを表している(式や定義から自明)。
「共分散」とは、ある多次元のデータ![]() に対して、平均
に対して、平均![]() または
または![]() からの差の積平均である。
からの差の積平均である。
式で書けば次のようになる。
![]()
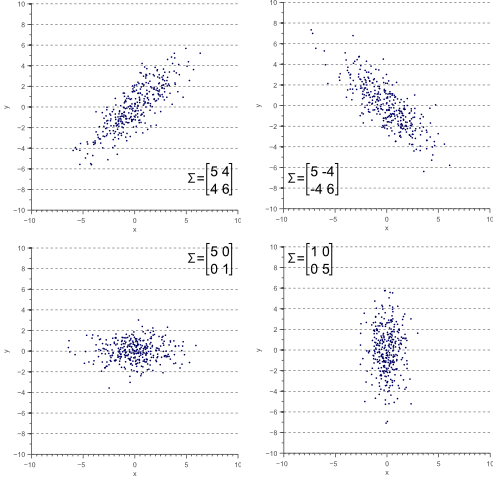
共分散は、xデータとyデータの相関度合いを示すものである。
さらに、「分散」と「共分散」を要素として並べた「共分散行列」は次のようになる。
![]()
![]()
共分散行列は行列の構成要素を「単に並べただけ」である。
何それ美味しいの?
例えば、下段の分布のように分散共分散行列の「共分散」部分が![]() の分布の場合、相関は見られない。
の分布の場合、相関は見られない。
要するに、共分散行列が分かると共分散行列に用いられている乱数の分布が分かる。
固有値・固有ベクトル
正方行列![]() (※縦の長さと横の長さが等しい行列)に対して、
(※縦の長さと横の長さが等しい行列)に対して、
![]()
となる ![]() を固有値(eigen value)、
を固有値(eigen value)、![]() を固有ベクトルと呼ぶ。
を固有ベクトルと呼ぶ。
![]() とは、「行列
とは、「行列 ![]() を掛けても、
を掛けても、![]() 倍されるだけで方向が変わらないベクトル」を意味する。
倍されるだけで方向が変わらないベクトル」を意味する。
例えば![]() が与えられた時、次の固有方程式
が与えられた時、次の固有方程式
(1) ![]()
を満たす固有値![]() と固有ベクトル
と固有ベクトル![]() を求めよ。
を求めよ。
という問題は、理系大学生なら解いた経験があるだろう。
「固有値問題」とは、この固有値・固有ベクトルを見つける問題である。
さらに、この2つの概念(共分散行列、固有値問題)を応用する例の1つが「主成分分析」である。
主成分分析(principal component analysis:PCA)とは?
与えられたデータの傾向から自動的に特徴量を見つけ出し、その特徴を良く表す低次元データへと次元圧縮を行うのが「主成分分析」である。
これはある種の機械学習であり、特に自動的に特徴量を見出すという点において、「教師なし学習」と分類される。
主成分分析(PCA)の目的
- データの特徴抽出(データのバラつきが大きい部分に着目することでよいデータを識別しやすくする)
- データの次元圧縮(データのバラつきが少ない部分はデータに共通するパターンなのであまり意味をなさない(無視))
- 多次元特徴量の可視化(多次元データは人間には認識不可、データのバラつきが大きところを見ることでデータの関係性を把握)
主成分分析がなぜ分散共分散行列を対角化する固有値問題となるか?
ここから本題。
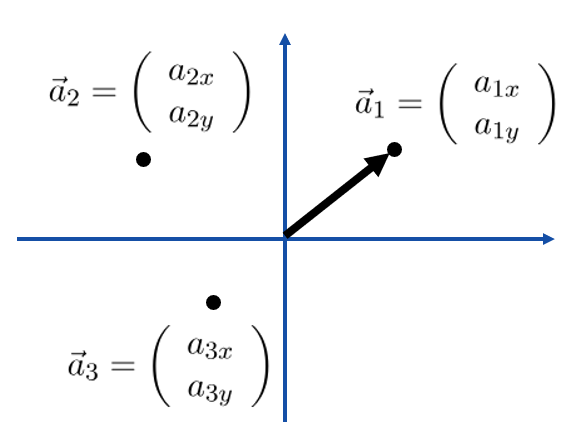
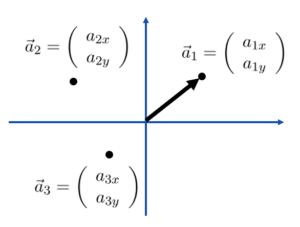
3つの二次元データ
![]()
についての主成分分析を考えてみよう。簡単のため、重心が原点(0,0)となるようなデータであるとしている。
今後のために、次のようにデータ成分を並べた行列を定義しておく。
(2) 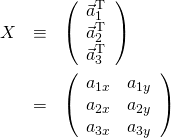
転置行列![]() との積
との積![]() を計算してみると、
を計算してみると、
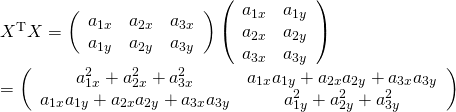
最終的な表式が、「共分散行列の形(1/データ数の因子を除く)」になっていることがわかる。
共分散行列は、以降のためにに![]() として定義しておく。
として定義しておく。
(3) ![]()
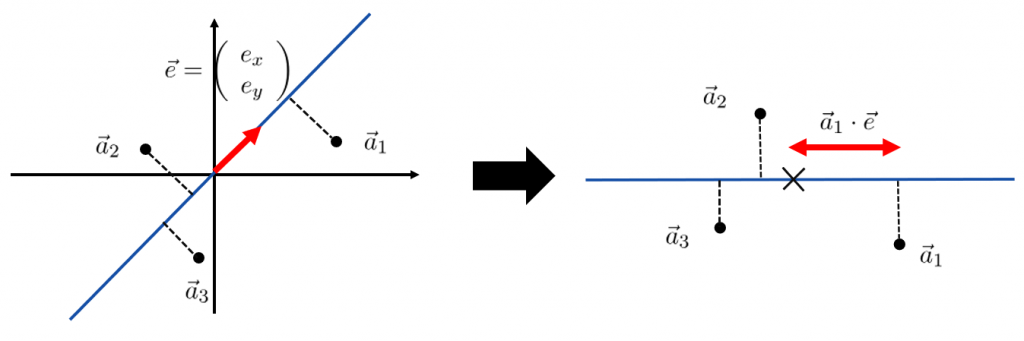
単位ベクトルにデータを射影した時の分散を計算
まず、データを![]() の方向に射影して、1次元データとなった後の分散値の表式を求める。
の方向に射影して、1次元データとなった後の分散値の表式を求める。
![]() を
を![]() に射影した値は
に射影した値は![]() のようにベクトルの内積を取ることで簡単に計算でき、これを用いて分散(var)を計算すると、次式になる(平均値は0となる)。
のようにベクトルの内積を取ることで簡単に計算でき、これを用いて分散(var)を計算すると、次式になる(平均値は0となる)。
(4) ![]()
これを行列の積の形に分解して表現してみると、次式になる。
実は、この分解した行列がそれぞれ(![]() )とその転置行列
)とその転置行列![]() になっている。
になっている。
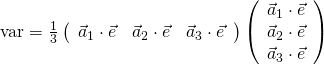
次に行列の性質を用いて、![]() という並びを出現させる。
という並びを出現させる。
(5) 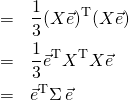
これは上で計算した共分散行列![]() である。
である。
varが最大になる方向を求める
さて、主成分分析ではこのvarを最大化するような![]() を求めることが目的であった。
を求めることが目的であった。
また、![]() には単位ベクトル、つまりノルムが1であるという制約条件も付いている。
には単位ベクトル、つまりノルムが1であるという制約条件も付いている。
このように、ある制約条件のもとで、関数の最大(最小)を決定する時には、「ラグランジュの未定乗数法」というものがよく用いられる。
ラグランジュの未定乗数法:
変数
について、「
」の制約条件下で「f(x,y)」という関数を最大(小)化するのは、
という関数を定義した時に、
を満たすような解
である。
ラグランジュの未定乗数法を用いると、
(6) 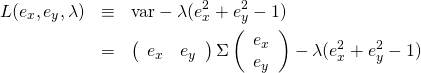
と定義した関数![]() に対して、
に対して、
(7) 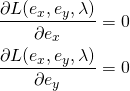
が成立するような![]() を見つければよい。
を見つければよい。
![]() ,
,![]() を計算すると、
を計算すると、
![]()
(8) ![Rendered by QuickLaTeX.com \begin{eqnarray*} &=& \left( \begin{array}{cc} 1 &0\end{array} \right) \Sigma \left( \begin{array}{c} e_{x} \\ e_{y} \end{array} \right) + \left[ \left( \begin{array}{cc} e_{x} & e_{y} \end{array} \right) \Sigma \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \right] ^{\mathrm{T}} - 2 \lambda e_x \\ &=& \left( \begin{array}{cc} 1 &0\end{array} \right) \Sigma \left( \begin{array}{c} e_{x} \\ e_{y} \end{array} \right) + \left( \begin{array}{cc} 1 &0\end{array} \right) \Sigma^\mathrm{T} \left( \begin{array}{c} e_{x} \\ e_{y} \end{array} \right) - 2 \lambda e_x \\ &=& 2 \left( \begin{array}{cc} 1 &0\end{array} \right) \Sigma \left( \begin{array}{c} e_{x} \\ e_{y} \end{array} \right) - 2 \lambda e_x \end{eqnarray*}](https://nehori.com/nikki/wp-content/ql-cache/quicklatex.com-d40e04ba66a5390bef36df9019bc8c6b_l3.png)
![]()
であり、これらが0になるので次式に変形できる。
(9) 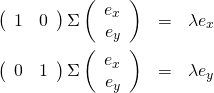
2つの方程式をまとめると次式になる。
(10) ![]()
一番左の行列はただの単位行列なので省略すると次式になる。
(11) ![]()
これは共分散行列Σに対する固有方程式である。
以上より、「主成分分析」が「固有値問題」へ帰着されることが証明された。