オルカンとS&P500を両方買うべきか？（効率的フロンティアをPython実装）

投資は「銘柄選び」ではない。

投資のリターンを左右するのは

アセットアロケーションが9割

だと言われている。

アセットアロケーションの最適化　ポートフォリオの構築とメンテナンスのための統合的アプローチ (ウィザードブックシリーズ Vol. 283) | ロバート・カーバー, 山下恵美子 |本 | 通販 | Amazon

Amazonでロバート・カーバー, 山下恵美子のアセットアロケーションの最適化　ポートフォリオの構築とメンテナンスのための統合的アプローチ (ウィザードブックシリーズ Vol. 283)。アマゾンならポイント還元本が多数。ロバート・カーバー, 山下恵美子作品ほか、お急ぎ便対象商品は当日お届けも可能。またアセットアロケー...

アセットアロケーションとは「株式、債券、現金などをどんな比率で持つか」ということだ。

この言葉は多くの書籍やブログに書かれている投資をする上で最初に学ぶべき言葉。

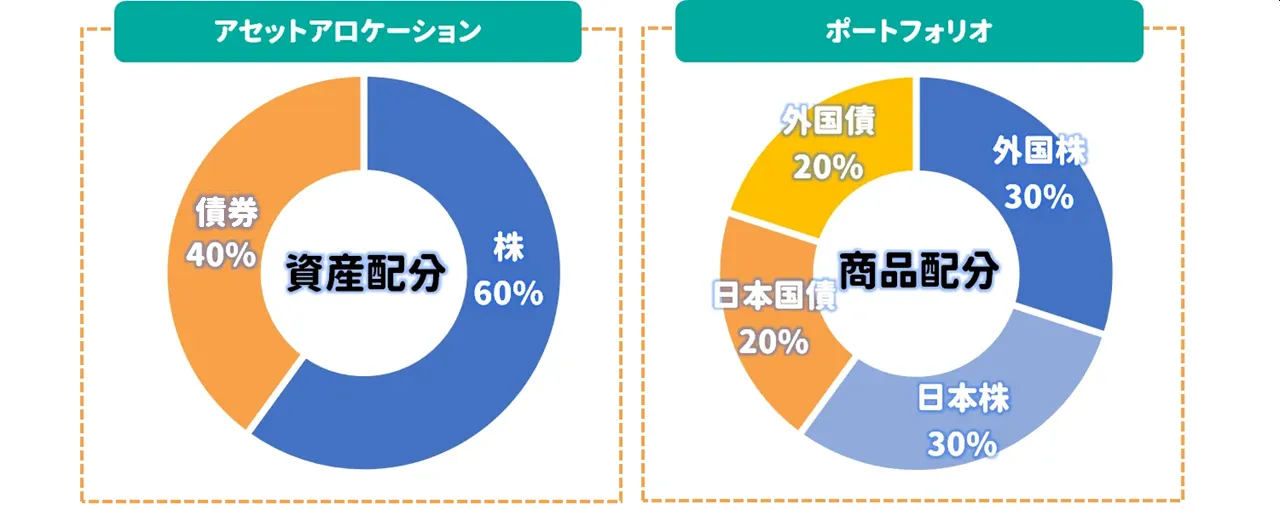
ちなみに、オルカン推奨派になる前の山崎元氏のオススメ資産配分比率は「日本株4：外国株6」で債券や金などは保有しない。無リスク資産は現金。

効率的フロンティアと資本市場線
おわりに
1. ソースコード

上記理由を説明するには

効率的フロンティア
資本市場線
接点ポートフォリオ

を理解する必要がある。

そもそも2級FP、証券アナリスト、中小企業診断士試験や大学授業でも「効率的フロンティア」「資本市場線」は出てくるので常識知識。

だけど、日々の飯をポストして講釈をたれてるFIRE投資家達の多くは、彼らのポートフォリオを見る限り知らないと思われる。

彼らのアドバイスは単なる感想文であり読むだけ無駄。

効率的フロンティアと資本市場線

元も子もないが、次の10分程度次の動画を見る方が私の説明聞くより何倍も良さそうだ。

【ファイナンス】効率的フロンティアと資本市場線の考え方をわかりやすく解説します！_ 財務会計_中小企業診断士試験対策

文章で長々と説明するより動画の方が分かり易い。

一応解説しておくと、

「効率的フロンティア」とは、同じリスクで最大のリターンを得るための証券の組み合わせ

「資本市場線」とは、安全資産も考慮した場合の最適な投資配分の組み合わせ

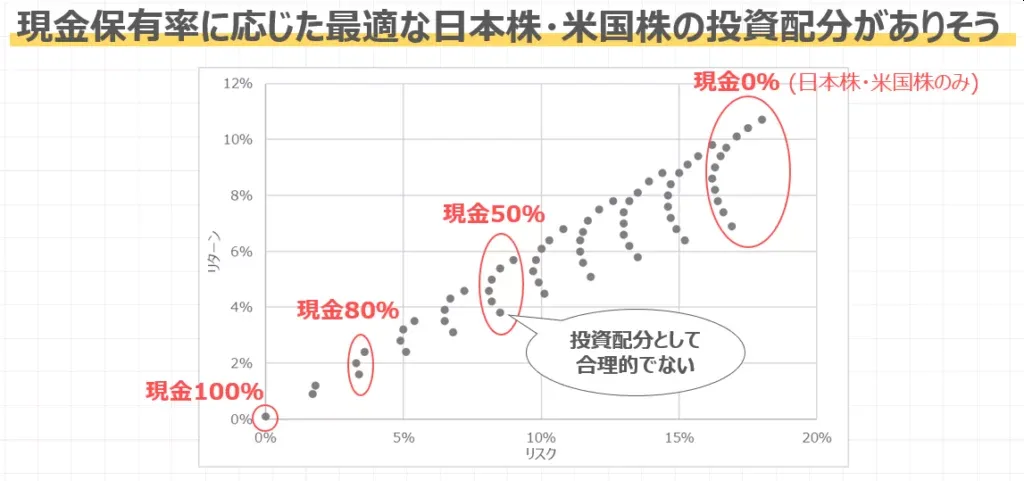
例えば米国株と日本株を保有する際に、現金保有と最適な投資配分が分かる。

そして、2つの交わる「接点（市場）ポートフォリオ」は「市場の全銘柄の加重平均」

つまり資産配分を考える際には、理論的にやるのなら上記のグラフを使い次のような検討を行う。

①株式や債券、不動産などの資産の中から「どのような資産を組み入れるか」を考える
②「組み入れた資産の配分比率をどうするか」ということを考える
③「自分が取れるリスク」や「求めるリターン」といった、投資家個人の事情を加える
④「自分が取れるリスクの範囲内で、リターンを最大化させるような資産の組み合わせ」を考える

なお、検索すると教科書的な資本市場線が出てくる。

が「リスクフリー（無リスク利子率）」は、

日本なら約0％
アメリカでは約2.4％（米国国債3ヵ月金利）

のため、座標軸が（0,0）から開始してない図は現実を直視できない学者資料だ。

数十年前に必死に利回り2%な貯金や預金があるのかと調べた記憶がある。まじで糞。

本当に成り立つのかPythonでシミュレーションしてみる

世の中、何でも疑ってかかろう。

接点ポートフォリオを求めるのは次の2つ。

オルカン（日本除く）
日本株

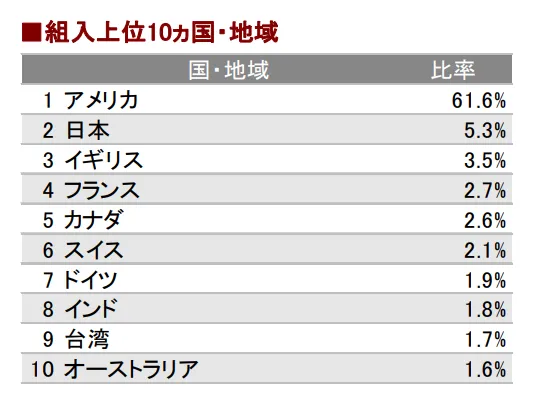
この比率はemaxis slim 全世界株式（オール・カントリー）の2024年5月の月報によると

日本株比率 5.3%

となっている。

シミュレーションして、この数字に近い結果になったら信じれるよね。

次の株価を利用してみた。

※ 実際にはMSCI Japan index（MSCIジャパンインデックス）を使う必要があるが株価データが見つからなかった

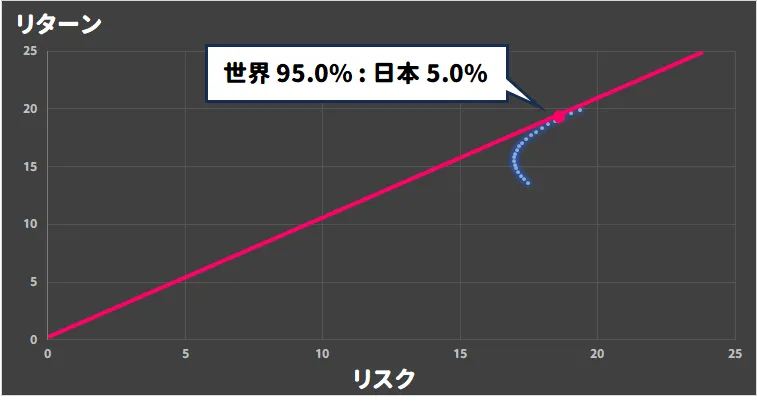
Pythonのシミュレーション結果、5年間の株価に基づく接点ポートフォリオの比率は次のようになった（2019年6月20日～2024年6月20日のデータ利用）。

95.0% MSCI World（世界）
5.0% TOPIX（日本）

素晴らしい。

ほぼ近い数字だと言って良いんじゃないかな。

「オルカンとS&P500」どっちが良い？どれだけ持てば良い？

よく見る討論。

そしてよく見る返答。

悩んで証券や生命保険会社のセミナーで質問したら別室に招かれて違う商品を買わされるなんて事も今まで何度も経験した。

リスク許容度が高い人も低い人も、リスク資産のポートフォリオの中身は同じで良い

これを「トービンの分離定理（ジェームス・トービン）」という

トービン金融論 | ジェームストービン, Tobin,James, 史郎, 薮下, 靖浩, 蟻川, 博, 大阿久 |本 | 通販 | Amazon

Amazonでジェームストービン, Tobin,James, 史郎, 薮下, 靖浩, 蟻川, 博, 大阿久のトービン金融論。アマゾンならポイント還元本が多数。ジェームストービン, Tobin,James, 史郎, 薮下, 靖浩, 蟻川, 博, 大阿久作品ほか、お急ぎ便対象商品は当日お届けも可能。またトービン金融...

「人によって違うから個別相談に来てね」という人間は僕は絶対に信じない。

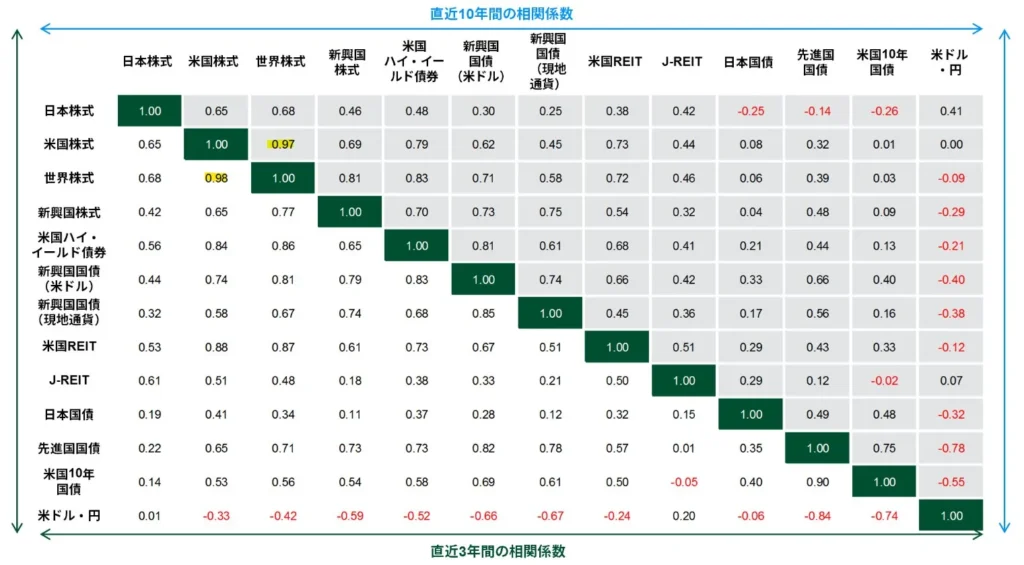
そもそも相関関係が極めて近いので、分散の観点で二つ持っててもあまり意味はない。

そして、これも「接点ポートフォリオ」を求める事で最適な比率が分かる。

ということで、やってみた。

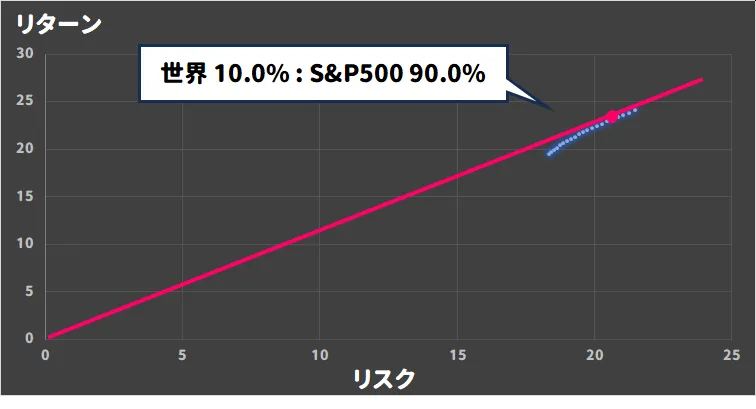
上記を使って最適なリスク・リターンとなる比率を求める（2020年1月7日～2024年6月20日のデータを利用）。

10.0% MSCI World（世界）
90.0% S&P500（米国）

なんと言うことでしょう……

50:50程度かと思いきや、オルカンなんて気持ち程度の組み込みでしかなく、大半がS&P500となってしまった。

市場が効率的だと仮定した場合の最も投資効率の良好な組み合わせ（オルカンとS&P500）は「10:90」。

どちらか一方の資産を持つなら

S&P500

が最適解。という結論が出てしまった……

ただしシャープ・レシオ（リスクに対するリターン）は

商品	年利リターン	年利リスク	シャープレシオ
米国株（S&P500）	24.08%	21.47%	1.1215
全世界（オルカン）	19.48%	18.34%	1.0626

であり、そもそもS&P500の方が最適な投資先と理論上はいえる。

「株と日本債券」をどれだけ持てば良い？

これもやってみた。

世界の株式・債券に6対4の割合で分散投資するのが伝統的な手法。

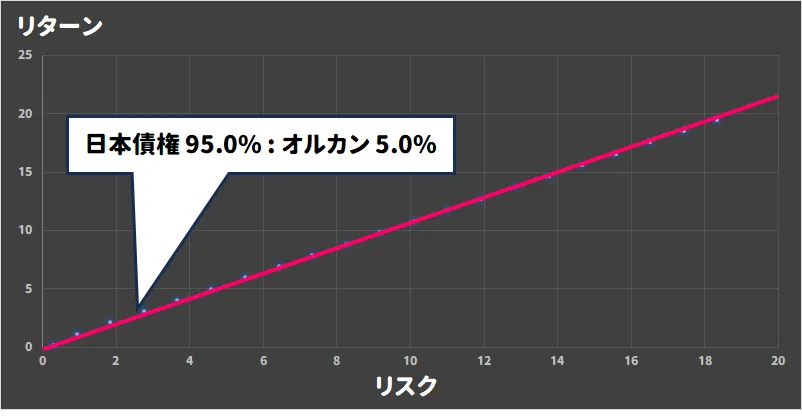
日本１０年債券利回りを使って実験。

5.0% 株（オルカン）
95.0% 債券（日本債券）

債券の年利が低すぎて効率的フロンティアが見えない……ひどすぎる。

なおシャープ・レシオ（リスクに対するリターン）は

商品	年利リターン	年利リスク	シャープレシオ
国内債券	0.19%	0.27%	0.6847
世界株	19.48%	18.34%	1.0626

であり、国内債券を買えばマイナスとなっている。

そして国内債券のリターン値が小さすぎて、リスクも小さいためにシャープ・レシオが高くなっているらしい。

ChatGPT-4oの返答はこちら。

リターンが非常に小さく、リスクも同様に小さい場合、シャープレシオが高くなる傾向があります

国債のような低リスク資産と株式のような高リスク資産を組み合わせると、ポートフォリオのリスクは低く抑えられ、シャープレシオが高くなる可能性があります。これは、効率的ポートフォリオ理論に基づく計算としては正しい結果と見なされます

そもそも計算ができないっぽいから、こっちは無視。

おわりに

市場が効率的だと仮定した場合、もっとも効率的なポートフォリオは「市場ポートフォリオ」である事は周知の事実。

ただし、最も投資効率の良好（低リスク高リターン）なのは

オルカンよりS&P500

と、この結果から言える。

分散されているからオルカン……と思ったけど、S&P500の方が良いと結論付けて良いの……かな。あれ？

ソースコード

利用方法。

python setten_portfolio2.py 1655.T.csv 2559.T.csv

1	python setten_portfolio2.py 1655.T.csv 2559.T.csv

import pandas as pd
import numpy as np
import csv
import sys

# CSVファイルからデータを読み込む関数
def load_data(file_name):
    df = pd.read_csv(file_name, parse_dates=['Date'])
    df.set_index('Date', inplace=True)
    df['Return'] = df['Close'].pct_change()
    return df['Return'].dropna()

# ポートフォリオのリターンを計算する関数
def calculate_portfolio_return(asset1_return, asset2_return, weight1):
    return weight1 * asset1_return + (1 - weight1) * asset2_return

# ポートフォリオのリスクを計算する関数
def calculate_portfolio_risk(asset1_risk, asset2_risk, weight1, covariance):
    weight2 = 1 - weight1
    portfolio_risk = np.sqrt((weight1 ** 2) * (asset1_risk ** 2) + 
                             (weight2 ** 2) * (asset2_risk ** 2) + 
                             2 * weight1 * weight2 * covariance)
    return portfolio_risk

# メイン関数
def main(file1, file2):
    # データを読み込む
    asset1 = load_data(file1)
    asset2 = load_data(file2)

    # 共分散行列を計算する
    returns_df = pd.DataFrame({file1: asset1, file2: asset2})
    cov_matrix = returns_df.cov()

    # 年率リターンとリスク（標準偏差）を計算する
    annualization_factor = 260
    mean_returns = returns_df.mean() * annualization_factor
    risks = returns_df.std() * np.sqrt(annualization_factor)

    # 共分散値を取得する
    covariance = cov_matrix.loc[file1, file2] * annualization_factor

    # リスクフリー金利を定義
    risk_free_rate = 0

    # 各資産のシャープレシオを計算する
    sharp_ratios_assets = (mean_returns - risk_free_rate) / risks

    # 計算した年利リターン、年利リスク、シャープレシオを表示
    print(f'{file1} 年利リターン: {mean_returns[file1]:.4f}, 年利リスク: {risks[file1]:.4f}, シャープレシオ: {sharp_ratios_assets[file1]:.4f}')
    print(f'{file2} 年利リターン: {mean_returns[file2]:.4f}, 年利リスク: {risks[file2]:.4f}, シャープレシオ: {sharp_ratios_assets[file2]:.4f}')

    # 効率的フロンティアを計算してCSVに出力する
    filename = 'efficient_frontier.csv'
    with open(filename, mode='w', newline='', encoding='shift_jis') as file:
        fieldnames = ['比率1', '比率2', 'ポートフォリオリターン', 'ポートフォリオリスク', 'シャープレシオ']
        writer = csv.DictWriter(file, fieldnames=fieldnames)
        
        writer.writeheader()
        for weight1 in np.arange(0, 1.05, 0.05):
            weight2 = 1 - weight1
            portfolio_return = calculate_portfolio_return(mean_returns[file1], mean_returns[file2], weight1)
            portfolio_risk = calculate_portfolio_risk(risks[file1], risks[file2], weight1, covariance)
            sharp_ratio = (portfolio_return - risk_free_rate) / portfolio_risk
            writer.writerow({
                '比率1': f'{weight1*100:.1f}%',
                '比率2': f'{weight2*100:.1f}%',
                'ポートフォリオリターン': portfolio_return,
                'ポートフォリオリスク': portfolio_risk,
                'シャープレシオ': f'{sharp_ratio:.3f}'  # 小数第3位まで丸める
            })

    # 資本市場線と接する接点ポートフォリオを計算する
    sharp_ratios = []

    for weight1 in np.arange(0, 1.05, 0.05):
        weight2 = 1 - weight1
        portfolio_return = calculate_portfolio_return(mean_returns[file1], mean_returns[file2], weight1)
        portfolio_risk = calculate_portfolio_risk(risks[file1], risks[file2], weight1, covariance)
        sharp_ratio = (portfolio_return - risk_free_rate) / portfolio_risk
        sharp_ratios.append((sharp_ratio, weight1, weight2))

    # 最大のシャープレシオを持つポートフォリオを見つける
    max_sharp_ratio, optimal_weight1, optimal_weight2 = max(sharp_ratios, key=lambda x: x[0])

    print(f'接点ポートフォリオの比率: {optimal_weight1*100:.1f}% {file1}, {optimal_weight2*100:.1f}% {file2}')
    print(f'ポートフォリオが {filename} として保存されました。')

if __name__ == "__main__":
    if len(sys.argv) != 3:
        print("Usage: python script.py <CSV file1> <CSV file2>")
    else:
        main(sys.argv[1], sys.argv[2])

import pandas as pd

import numpy as np

import csv

import sys

# CSVファイルからデータを読み込む関数

def load_data(file_name):

df = pd.read_csv(file_name, parse_dates=['Date'])

df.set_index('Date', inplace=True)

df['Return'] = df['Close'].pct_change()

return df['Return'].dropna()

# ポートフォリオのリターンを計算する関数

def calculate_portfolio_return(asset1_return, asset2_return, weight1):

return weight1 * asset1_return + (1 - weight1) * asset2_return

# ポートフォリオのリスクを計算する関数

def calculate_portfolio_risk(asset1_risk, asset2_risk, weight1, covariance):

weight2 = 1 - weight1

portfolio_risk = np.sqrt((weight1 ** 2) * (asset1_risk ** 2) +

(weight2 ** 2) * (asset2_risk ** 2) +

2 * weight1 * weight2 * covariance)

return portfolio_risk

# メイン関数

def main(file1, file2):

# データを読み込む

asset1 = load_data(file1)

asset2 = load_data(file2)

# 共分散行列を計算する

returns_df = pd.DataFrame({file1: asset1, file2: asset2})

cov_matrix = returns_df.cov()

# 年率リターンとリスク（標準偏差）を計算する

annualization_factor = 260

mean_returns = returns_df.mean() * annualization_factor

risks = returns_df.std() * np.sqrt(annualization_factor)

# 共分散値を取得する

covariance = cov_matrix.loc[file1, file2] * annualization_factor

# リスクフリー金利を定義

risk_free_rate = 0

# 各資産のシャープレシオを計算する

sharp_ratios_assets = (mean_returns - risk_free_rate) / risks

# 計算した年利リターン、年利リスク、シャープレシオを表示

print(f'{file1} 年利リターン: {mean_returns[file1]:.4f}, 年利リスク: {risks[file1]:.4f}, シャープレシオ: {sharp_ratios_assets[file1]:.4f}')

print(f'{file2} 年利リターン: {mean_returns[file2]:.4f}, 年利リスク: {risks[file2]:.4f}, シャープレシオ: {sharp_ratios_assets[file2]:.4f}')

# 効率的フロンティアを計算してCSVに出力する

filename = 'efficient_frontier.csv'

with open(filename, mode='w', newline='', encoding='shift_jis') as file:

fieldnames = ['比率1', '比率2', 'ポートフォリオリターン', 'ポートフォリオリスク', 'シャープレシオ']

writer = csv.DictWriter(file, fieldnames=fieldnames)

writer.writeheader()

for weight1 in np.arange(0, 1.05, 0.05):

weight2 = 1 - weight1

portfolio_return = calculate_portfolio_return(mean_returns[file1], mean_returns[file2], weight1)

portfolio_risk = calculate_portfolio_risk(risks[file1], risks[file2], weight1, covariance)

sharp_ratio = (portfolio_return - risk_free_rate) / portfolio_risk

writer.writerow({

'比率1': f'{weight1*100:.1f}%',

'比率2': f'{weight2*100:.1f}%',

'ポートフォリオリターン': portfolio_return,

'ポートフォリオリスク': portfolio_risk,

'シャープレシオ': f'{sharp_ratio:.3f}' # 小数第3位まで丸める

})

# 資本市場線と接する接点ポートフォリオを計算する

sharp_ratios = []

for weight1 in np.arange(0, 1.05, 0.05):

weight2 = 1 - weight1

portfolio_return = calculate_portfolio_return(mean_returns[file1], mean_returns[file2], weight1)

portfolio_risk = calculate_portfolio_risk(risks[file1], risks[file2], weight1, covariance)

sharp_ratio = (portfolio_return - risk_free_rate) / portfolio_risk

sharp_ratios.append((sharp_ratio, weight1, weight2))

# 最大のシャープレシオを持つポートフォリオを見つける

max_sharp_ratio, optimal_weight1, optimal_weight2 = max(sharp_ratios, key=lambda x: x[0])

print(f'接点ポートフォリオの比率: {optimal_weight1*100:.1f}% {file1}, {optimal_weight2*100:.1f}% {file2}')

print(f'ポートフォリオが {filename} として保存されました。')

if __name__ == "__main__":

if len(sys.argv) != 3:

print("Usage: python script.py ")

else:

main(sys.argv[1], sys.argv[2])