画像認識は専門だったけど、音声認識はよく知りません。
「フーリエ変換」使うんでしょ?
昔は計算式の勉強が必要だったけど、今はPythonのライブラリで一発変換なんじゃないの?
ぐらい。
時間もスキルも無いが、簡単に基礎を理解しておく。
フーリエ変換(Fourier transform)とは何か?
「音」は様々な音が混ざり合っています。
この複雑なよりをほどいていくと単純な純音の集合となります。
例えば種類の違う正弦波がいっぱいあって、同時にスピーカーから音を出したらどうなるでしょう?
実際には音は合成されて、こんな波形になります。
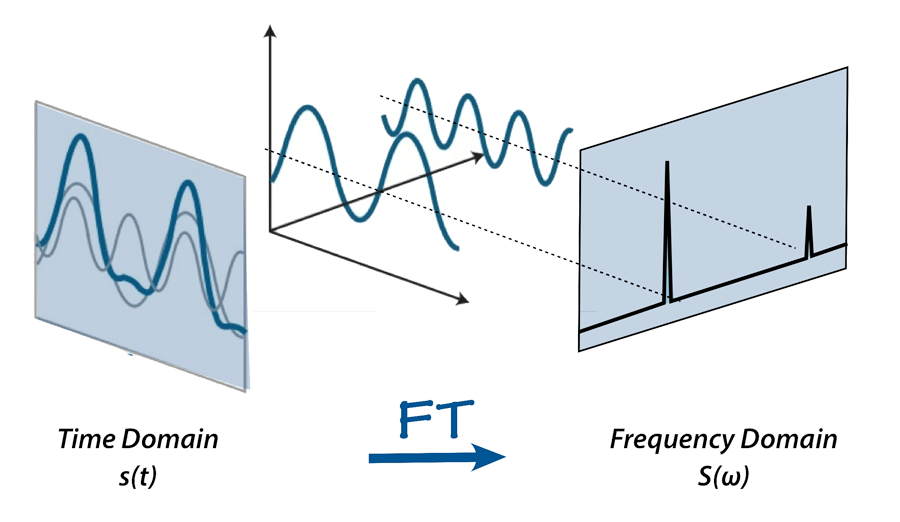
ある波形を「フーリエ変換」すると、その波形の中に何 Hz の波が含まれているかが分かります。
要するに、フーリエ変換とは、
時間領域から周波数領域に変換することで、
その波形がどんな波によりどれくらいの割合で構成されているか?
を教えてくれる処理です。
文脈などによっては、フーリエ変換 と言って、高速フーリエ変換(FFT) や 離散フーリエ変換(DFT)の事を指すことがあります。
| 時間領域 | 名前 | 周波数領域 | ||
|---|---|---|---|---|
| 連続 | 周期的 | フーリエ級数展開 | 離散的 | 非周期的 |
| 連続 | 非周期的 | フーリエ変換(FT) | 連続 | 非周期的 |
| 離散的 | 非周期的 | 離散時間フーリエ変換(DTFT) | 連続 | 周期的 |
| 離散的 | 周期的 | 離散フーリエ変換(DFT) | 離散的 | 周期的 |
フーリエ変換は数学的な技法で、離散フーリエ変換(DFT)はコンピューター計算をする時のものです。
数学では単に連続な値を用いていますが、コンピュータではもちろんそんな無限個の数字とかは用意出来ません。
そのため、離散的な数字を使って、コンピュータでもフーリエ変換を行えるようにしたのが、離散フーリエ変換(DFT)です。
離散的な数字というのは、ようするに「現実的に取得可能なデータ群」ということです。
何となく理解すれば、あとはライブラリが勝手に変換するので数式は記載しない。
Pythonを使って具体的に見てみる
実際に見てみた方が早そうです。
必要なライブラリは次の通りです。
|
1 2 3 4 |
pip install numpy pip install librosa pip install matplotlib pip install scipy |
LibROSAは、信号処理、音の分析につかうパッケージです。
なお、動作確認はWindows上で行っています。
今回はMatplotlibの日本語文字化けを、fontname使って回避しているのでLinuxユーザは日本語表記が出来ないです。
音声データは、動物「犬」のファイルを使いました。
ただステレオには非対応なので、モノラル変換が必要です(詳細は後述しています)。
音声データを表示
まず最初に音声データの中身をそのまま表示してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import sys import scipy.io.wavfile import numpy as np import matplotlib.pyplot as plt #音声ファイル読み込み args = sys.argv wav_filename = args[1] rate, data = scipy.io.wavfile.read(wav_filename) ##### 音声データをそのまま表示する ##### #縦軸(振幅)の配列を作成 #16bitの音声ファイルのデータを-1から1に正規化 data = data / 32768 #横軸(時間)の配列を作成 #np.arange(初項, 等差数列の終点, 等差) time = np.arange(0, data.shape[0]/rate, 1/rate) #データプロット plt.plot(time, data) plt.title('音声データの中身' ,fontname="MS Gothic") plt.xlabel('周波数' ,fontname="MS Gothic") plt.ylabel('振幅' ,fontname="MS Gothic") plt.show() |
ここで、
rateは一秒間にサンプリングされる回数(サンプリング周波数)
dataはサンプリング時の振幅(音量)
です。

上記のプログラム実行時に音声ファイルのパスを引数に指定すると、
|
1 |
% python sample.py doga.wav |
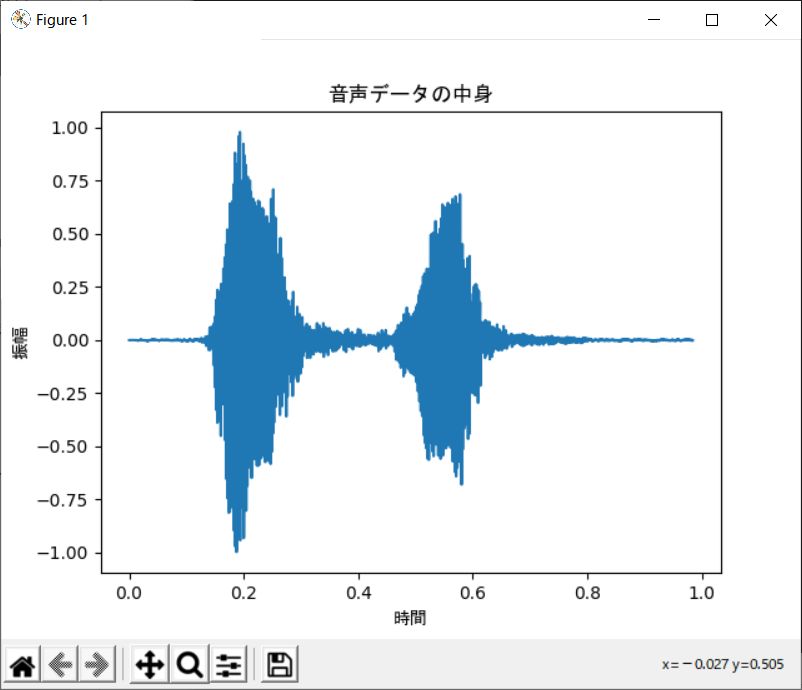
次のようなグラフが表示されます。
横軸が時間、縦軸が振幅です。
WAV上では「ワンワン」と犬が二回吠えてますが、一回目と二回目で振幅が異なることが分かります。
ただ、これだと音声データが波になっていることがわかりません。
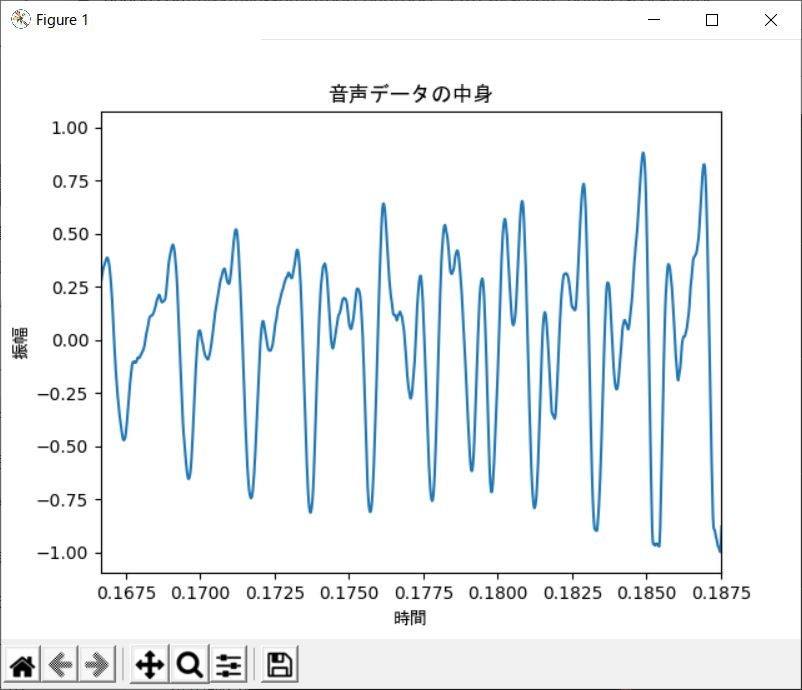
このためグラフを拡大し、最初の8000~9000サンプルのデータを見てみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import sys import scipy.io.wavfile import numpy as np import matplotlib.pyplot as plt #音声ファイル読み込み args = sys.argv wav_filename = args[1] rate, data = scipy.io.wavfile.read(wav_filename) ##### 音声データをそのまま表示する ##### #縦軸(振幅)の配列を作成 data = data / 32768 #横軸(時間)の配列を作成 #np.arange(初項, 等差数列の終点, 等差) time = np.arange(0, data.shape[0]/rate, 1/rate) #データプロット plt.plot(time, data) plt.xlim(8000/rate, 9000/rate) plt.title('音声データの中身' ,fontname="MS Gothic") plt.xlabel('時間' ,fontname="MS Gothic") plt.ylabel('振幅' ,fontname="MS Gothic") plt.show() |
plt.xlim(Xの最小値, Xの最大値)
で、軸の範囲を限定しています。
次のように表示されます。
確かに波になっている事が確認できました。
周波数成分を表示
続いて、高速フーリエ変換(fast Fourier transform, FFT)を用いてこの音声データの周波数成分を求めてみます。
前述通り、高速フーリエ変換は、離散フーリエ変換(discrete Fourier transform, DFT)を計算機上で高速に計算するアルゴリズムです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
import sys import scipy.io.wavfile import numpy as np import matplotlib.pyplot as plt #音声ファイル読み込み args = sys.argv wav_filename = args[1] rate, data = scipy.io.wavfile.read(wav_filename) #(振幅)の配列を作成 data = data / 32768 ##### 周波数成分を表示する ##### #縦軸:dataを高速フーリエ変換する(時間領域から周波数領域に変換する) fft_data = np.abs(np.fft.fft(data)) #横軸:周波数の取得 #np.fft.fftfreq(データ点数, サンプリング周期) freqList = np.fft.fftfreq(data.shape[0], d=1.0/rate) #データプロット plt.plot(freqList, fft_data) plt.title('周波数成分' ,fontname="MS Gothic") plt.xlabel('周波数' ,fontname="MS Gothic") plt.ylabel('振幅' ,fontname="MS Gothic") plt.xlim(0, 8000) #0~8000Hzまで表示 plt.show() |
PythonモジュールNumpy「numpy.fft.fft」を用いることで高速フーリエ変換を実装できます。
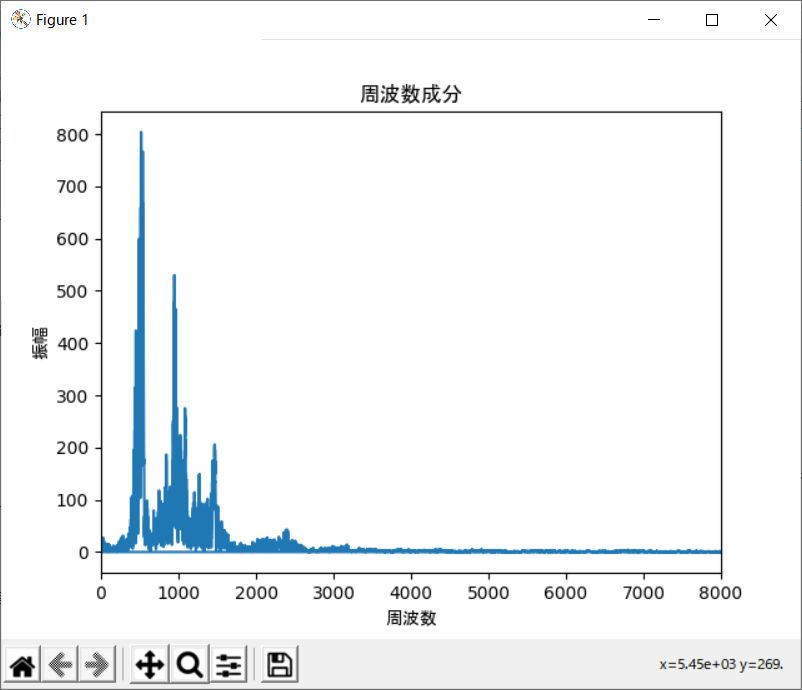
音声ファイルを指定してこのプログラムを実行してみると、次のようなグラフが表示されます。
横軸が周波数、縦軸が振幅です。
周波数とは電気振動などの現象が、1秒間当たりに繰り返される回数のことです。
「500Hz」「1000Hz」に集中していることが分かります。
「ワン」「ワン」の「ワ」と「ン」の周波数が異なるため、このようなグラフになっていると思われます。
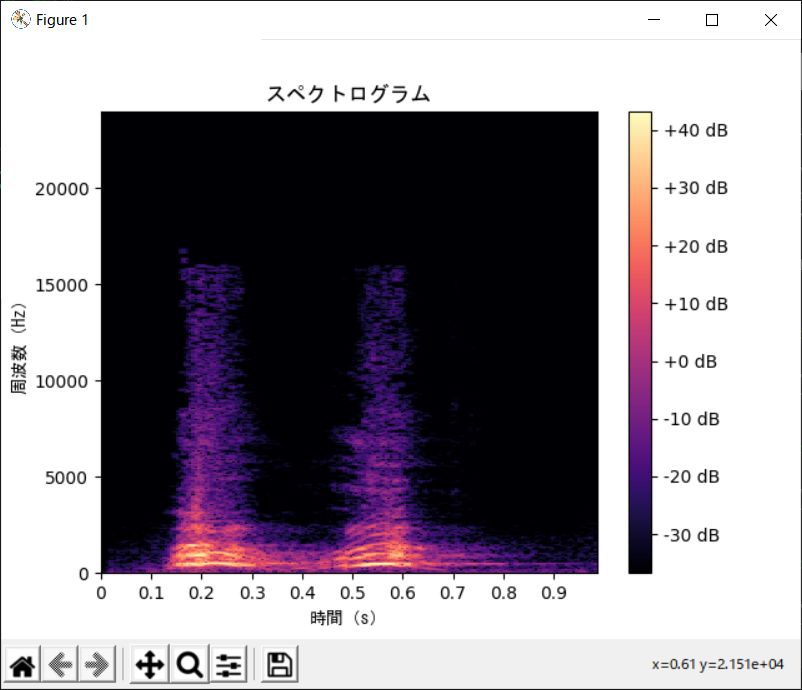
スペクトログラム(Spectrogram)を表示
高速フーリエ変換では音声データを時間領域から周波数領域に変換するだけなので「どの時間にどのような周波数が含まれているのか」が分かりません。
それを視覚化するヒートマップとして「(サウンド)スペクトログラム」というものがあります。
各軸は次から構成されています。
横軸・・・時間
縦軸・・・周波数スペクトル
これで、
どの時間にどのような周波数がどれくらい含まれているのか
がわかります。
プログラムは次のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import sys import numpy as np import librosa import matplotlib.pyplot as plt import scipy.io.wavfile import librosa.display #音声ファイル読み込み args = sys.argv wav_filename = args[1] rate, data = scipy.io.wavfile.read(wav_filename) #16bitの音声ファイルのデータを-1から1に正規化 data = data / 32768 # フレーム長 fft_size = 1024 # フレームシフト長 hop_length = int(fft_size / 4) # 短時間フーリエ変換実行 amplitude = np.abs(librosa.core.stft(data, n_fft=fft_size, hop_length=hop_length)) # 振幅をデシベル単位に変換 log_power = librosa.core.amplitude_to_db(amplitude) # グラフ表示 librosa.display.specshow(log_power, sr=rate, hop_length=hop_length, x_axis='time', y_axis='hz', cmap='magma') plt.colorbar(format='%+2.0f dB') plt.title('スペクトログラム' ,fontname="MS Gothic") plt.show() |
通常、フーリエ変換は信号の全時間にわたって計算を行いますが、時間ごとに周波数に関する情報が欲しい場合は適しません。
そういった場合に、短い区間に対するフーリエ変換を繰り返します。これが短時間フーリエ変換(STFT)です。
これで、
その短時間の音がどのような周波数からできているか
が分かります。
次のようなグラフが出力されます。
これで「時間」に対する「周波数」を画像として表現できるようになりました。
【エラー】Invalid shape for monophonic audio
実行した際に次のようなエラーが出ました。
|
1 2 |
raise ParameterError( librosa.util.exceptions.ParameterError: Invalid shape for monophonic audio: ndim=2, shape=(21888, 2) |
このプログラムでは、2チャンネル(ステレオ)は処理できないので、1チャンネル(モノラル)に変換する必要があります。
下記のサイト等でモノラルに変換できます。

メル スペクトログラム(Mel* Spectrogram)を表示
メルスペクトログラムは、周波数がメルスケールに変換されているスペクトログラムです。
メルスペクトログラムへ変換することにより、次の効果があります。
- 次元が下がる
- 低音域では敏感に、高音域では鈍感になる(人間の耳の仕様に近づく)
プログラムは次のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import sys import numpy as np import librosa import matplotlib.pyplot as plt import scipy.io.wavfile import librosa.display #音声ファイル読み込み args = sys.argv wav_filename = args[1] rate, data = scipy.io.wavfile.read(wav_filename) #16bitの音声ファイルのデータを-1から1に正規化 data = data / 32768 # フレーム長 fft_size = 1024 # フレームシフト長 hop_length = int(fft_size / 4) # 短時間フーリエ変換実行 amplitude = np.abs(librosa.stft(data, n_fft=fft_size, hop_length=hop_length)) # decibel単位に変換 log_power = librosa.core.amplitude_to_db(amplitude) # 振幅をデシベル単位に変換 melsp = librosa.feature.melspectrogram(S=log_power, n_mels=128) # グラフ表示 librosa.display.specshow(melsp, sr=rate, hop_length=hop_length, x_axis="time", y_axis="mel", cmap='magma') plt.colorbar(format='%+2.0f dB') plt.title('メル スペクトログラム' ,fontname="MS Gothic") plt.xlabel('時間(s)' ,fontname="MS Gothic") plt.ylabel('周波数(Hz)' ,fontname="MS Gothic") plt.show() |
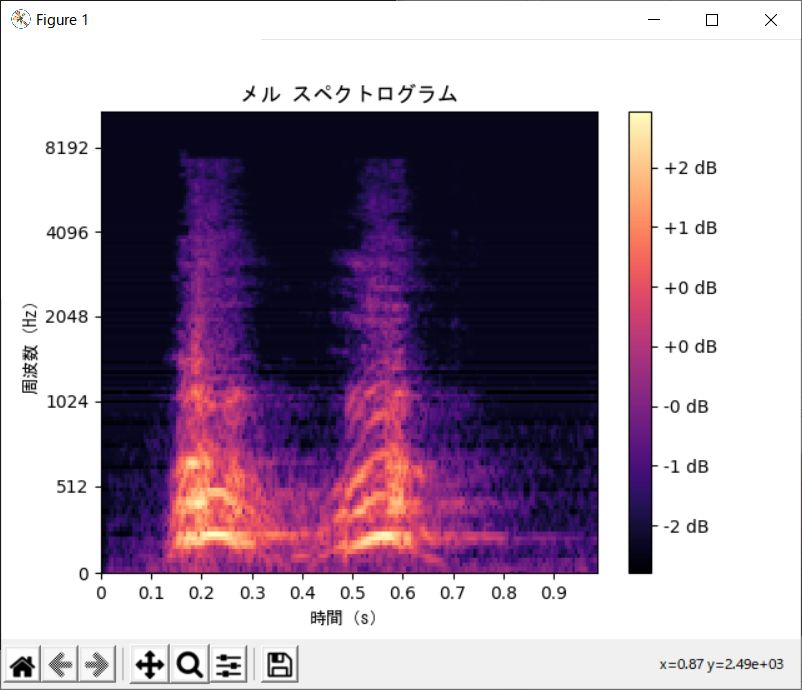
次のようなグラフが出力されます。
うーん、なんか違う気がする・・・・。
メル周波数スペクトログラム(Mel* frequency spectrogram)
メル周波数スペクトログラムは、以下の手順で算出することができます。
- 音声フレームに窓関数を適応し、離散フーリエ変換してパワースペクトルを得る
- メル周波数で均等になるようにスムージングする
ここは後日、心に余裕があれば検討するか・・
そもそも、、
- メル尺度(メルスケール)・・・・・音高の知覚的尺度(メル尺度の差が同じであれば、人間が感じる音高の差が同じになる)
- バーク尺度(バークスケール)・・・音響心理学的尺度。メル尺度の方がバーク尺度よりもよく使われている
- ケプストラム・・・・・・・・・・・音声を音の発生源の周波数と声道の周波数に分解するための処理
- メル周波数ケプストラム(MFCC)・・メルスペクトラムの各時間フレーム毎に、離散コサイン変換、ローパスリフタリングを行う
MFCCは楽器音に対しては音色に対応しており、音色が異なるとMFCCの形状は異なることが期待らしいが・・・、
難しいんだよ。。イミフ。
まとめ
実装コードはどこかのサイトのものを丸パクリしています。
最初はスペクトログラムを作る目的がよく分かりませんでしたが、画像上に音声の特徴をできる限り表現するため・・だと思ってます。
つまり、スペクトログラムの画像には音声の特徴が現れているため、畳み込みニューラルネットワーク(CNN)の訓練データとして使うことができます。
なお、メルスペクトログラムは音声認識では適していますが、自然界の音はスペクトログラムの方がCNNの精度が高い場合もあります。
また、音ファイルでは「バッチノーマライゼーション(Batch Normalization)」が効果的と記載しているサイトもありました。