小学校3年「3.9+5.1=9.0は減点」に対する歴史的背景と個人的見解

定期的に話題になる小学校教育問題。そして今ホットな話題は次のツイッター。

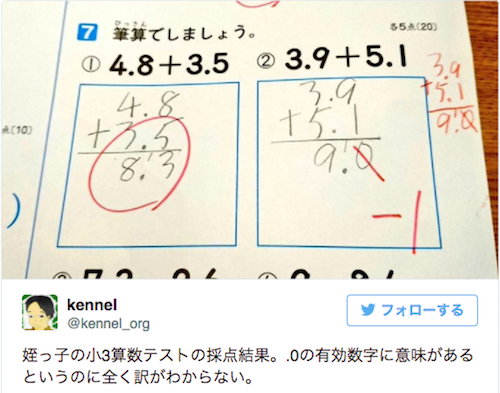
姪っ子の小3算数テストの採点結果。.0の有効数字に意味があるというのに全く訳がわからない。

写真には「3.9+5.1=9.0」とした解答に対し、赤ペンで小数点第１位の「0」の部分に斜線が引かれ、「-1」と減点されています。

こちらの対応に対して賛否両論で激しいバトルが繰り広げられているようです。

既に塾講師やフィールズ賞受賞者など権威ある人までが発言をしていますが、臆する事なく自分の意見を書いてみようと思います。

否定派

• 林 修さん（東進ハイスクール講師）
• 森 重文さん（フィールズ賞受賞者）
• 茂木 健一郎さん（ソニーコンピュータサイエンス研究所上級研究員）

などなど豪華なメンバーです。

林修さん「5.9と3.1で9.0になったらこの0は決して9という正数として扱わなければダメだっていうふうに押し付けるんですけど。それを押し付ける人はたぶんあの式の意味が分かっていない。教える側が数学の本質をわからないまま教えている可能性がある。」

森重文さん「もし最初に”できるだけ簡潔な表現をしろ”と条件が入っていれば、“9.0”を減点することはあり得るが、僕の感覚ではそれはない。減点はしないですけど。」
林修さん「どちらでもいいという判断？」
森重文さん「当然そうですね。何がいかんのだ？という感じですけど。」

【引用】毎日放送「林先生が驚く初耳学」　2016年12月25日

という意見や、茂木さんは文科省に喧嘩を売ってます。。

小学校算数の奇習が一部でまかり通っている現状を改善するには、そんなもん、一瞬たりとも意味がない、という観念、情報を、折りに触れ拡散する必要があるだろうし、また、文科省にも、きちんとした対応をとっていただきたいと思う今日この頃である。

ふしぎに思うのは、ぼくが小学生の頃は、「小数点」「かけ算の順序」「たし算の順序」といった問題は経験した記憶がないということで、いつからそんな奇習が小学算数の一部に広がってしまったのだろう。もしそんなものがあったら、小学生のぼくはかなり深刻な大人不信になっていたと思う。

【引用】小学校の算数にまかり通っている「奇習」は、子どもたちに対する「虐待」である　（茂木 健一郎）2016年11月21日

要するに、小数点以下に0を付ける表記法が現実に普通に存在してるのに、0に斜線をつけなければ減点するという採点基準なり教え方がおかしいから改善すべき。

という意見です。

擁護派

擁護派の意見の代表例が次のとおり（著名人で擁護派がいれば教えてください）。

算数が苦手な生徒を教えていたときに、気づいたことがある。彼らは、公式の計算方法は知っていても、その意味については理解できていないのだ。

「たかしくんはいくつかりんごを持っています。たかしくんは、持っているりんごを3つ食べました。食べたあとには、りんごは1つ残っています。はじめに持っているりんごはいくつでしょう」

と、問題を複雑にすると

3-1 = 2

などと間違えるのである。

これは、この子供が問題文を理解した上で計算を行っているのではなく、「問題文に出てくる数字」を、「足す引くを問題文の雰囲気から想像して」、「問題文に出てくる順番」で計算していることが原因である。

【引用】足し算の順序にこだわる理由と、それでも言いたいこと（mahiru123）

結論として、この教育は、初期段階で今後の文章題に対応する力をつけるためのものだということです。

前提知識

私も当初は「3.9 + 5.1 = 9.0」が減点になる理由が分かりませんでした。

なぜなら、数学の世界では次は公理だからです。

9 = 9.0

ただし、この議論の本質に迫るには、いくつかの前提を理解する必要があります。

【2023.06.30】この考えは「間違い」だとの指摘が入りましたので追記しておきます。

「小数点」問題はいつから存在しているのか？

戦前から日本の教科書では9.0は9に直すと書かれています。

例えば、大正15年の児童用算術書（副算術書）「欧米小学算術書. 上級編（5・6学年） 上」（阿部八代太郎監修、国元東九郎, 小島ミサヲ 訳）の「小数の加法」には次のように書かれています。

5.90といわないで5.9といいます。
10.0米といわないで、10米といいます。

因みに、監修、訳者は次のような方々です。

• 阿部八代太郎（1883〜1951年）さんは、欧米に留学後、東京物理学校(現東京理大)教授、日本数学教育学会会長
• 国元東九郎（1894〜1985年）さんは、東京高等師範学校の数学専攻で、学習院の教授

この算術書は欧米の教科書を範としています。要するに日本の教育が特別おかしいのではありません。

そして茂木さんは幼少期は春日部市で育ったらしいので同様に学んでるはずです。

日本での指導方針は戦前から変わっていません。

【補足】有効数字上は9.0こそ正解では？

色々なコメントを見てみると、エンジニアやら物理や化学を学んだ人々が「有効数字」を持ち出して次のように発言しています。

「9ではなく、むしろ9.0こそが正解だ！」

むしろ、こちらの方が問題発言です。

一般社会の数字で.0を残すのは有効数字という考え方がもとになっています。

ただし、有効数字は誤差を含む数字にのみ考えられる概念です。

例えば、次のように有効数字に基づいて正しく計算しました。でも、これは小学校算数・数学では正解になりません。

1.1 + 1.11 = 2.2

再度いいますが、算数・数学の数字は誤差を含まない数字であり、次は公理です。

9 = 9.0

「算数」とは何か？

この議論の本質を考えるためには「数学」と「算数」が違うことを、まず理解しないと始まりません。

「算数」は、小学校教育の次の目標を達成する観点から編成されています。

日常生活に必要な数量的な関係を、正しく理解し、処理する能力を養うこと
(学校教育法 18)

このために、名前も明治・大正時代の計算を主とした「算術」から、数量や図形を広く取扱い数理思想の開発を重視する意味で1941年より「算数」に変わりました。

要するに「算数」では単純に答えをだすのではなく、

考え方や課程を理解するための「答えに至るまでのプロセス」

が重視されます。

その上で、文部科学省教育課程課では、次のようにルールを定めています（ただし明記なし）。

原則として算数は数字を簡単に記すルールがある

つまり、算数では「3.9+5.1=9」と答えてもらうことが期待値なのです。

「9.0」の場合は途中で終わっている、最後まで計算されていないとされ、消し忘れ扱いで減点対象となっています。

授業でもそのように説明しており、森重文先生自身も上記で認めています。

「『できるだけ簡潔な表現をしろ』と条件が入っていれば、『9.0』を減点することはあり得る」

以上を踏まえた上での個人的見解

数学の教員免許状、専修免許状を取得しているだけのサラリーマンである私の考えです。

私が問題視すべき内容は次の4点だと考えています。

• 1. 現場の裁量任せでいいのか？
• 2. 明確なルールを定めるべきか？
• 3. 簡潔に書くというルールは必要なのか？
• 4. 教育という点ではどうしたらいいのか？

小学生はこの小数の計算の習得に何週間もかけます。

そのような小学生が間違いなく解けるように工夫した結果が、現在の指導方法という理解です。

著名人達は数学としての正しさに焦点がいってますが、

教育上のどのような指導が合理的か？

という話には及んでいません。

有識者達は「奇習」とBlogやテレビで文句を言うのではなく、是非、未来の小学生たちの為に数学習得に向けた学習指導要領を一緒に考えて頂きたいです。

前述したように、原則として算数は数字を簡単に記すルールがあります。

※ 分数は約分し、既約分数で答えます。

これは、小学生が数量を正しく理解し、答えに至るプロセスを学ぶために必要なルールだと理解しています。

そして、これは多くの数学者達と長い間議論された上で決められた方針です。

小数点以下の末尾0の扱いについては、単に消すか消さないかというだけではなく、小数の意味そのものに戻って教える必要があります。

子どもは意味を伴って理解しています。そして、学生のノートブックを見ると、解き方・概念を先生から学んでいるはずです。

【私の結論】

私が小学校の先生であれば、授業で習った「9.0 = 9」の概念を理解しているか確認する上で減点します（それが教科書の方針のため）

※ 「9.0の0の部分に斜線を引く」指導していた場合には、答えを9と書いても減点します。

ただし、私も小学生時代に、X、Yの方程式を使って鶴亀算を解いてバツになった経験もあり算数に理不尽さは持っています。

でも何度も言いますが、下記を忘れてはいけません。

小学校はプロセス（課程）を学ぶ場所（頑張りを評価）

中学生は結果を出すことを学ぶ場所（正しさを評価）