8回目で精度の高い学習モデルを構築するために「交差検証」「ROC 曲線とAUC」について実装追加しました。
11回目ではファンダメンタルズ指標を追加することで「AUC=0.70」を超えました。
- 【12回目】機械学習を使った株価予測(pandas-profiling、create_tree_digraphで可視化する)
- 【11回目】機械学習を使った株価予測(ファンダメンタルズ指標導入でAUC=0.70超え)
- 【10回目】機械学習を使った株価予測(関連論文・サイトを調査してみる)
- 【9回目】機械学習で株価予測(年利・勝率向上の分析)
- 【8回目】機械学習で株価予測(交差検証+ROC 曲線とAUCで脱過学習)
- 【7回目】機械学習で株価予測(騰落レシオ+株価分割対応で複数銘柄)
- 【6回目】機械学習で株価予測(機械学習で株予測(3点チャージ法の有効性検証)
これは、無謀にも「株の自動売買で億り人」を夢見て人生を浪費している一人の中年男の物語です。
今回は学習モデルの「ハイパーパラメータの調整」を実装を学び、加えて過学習の抑制についても検討してみます。
パラメータのチューニング
パラメータとは機械学習モデルにおける設定値や制限値のことです。ハイパーパラメータとも呼びます。
そして、モデルが最適解を出せるパラメータを走査し、設定することを「パラメータチューニング」といいます。
代表的なチューニング方法として2種についてまとめます。
グリードサーチ/ランダムサーチ
グリッドサーチは、あらかじめパラメータの候補値を指定し、その候補パラメータを組み合わせて学習を試行することにより最適なパラメータを走査する方法です。
ランダムサーチは、パラメータの設定範囲および試行回数を指定し、指定値範囲内から無作為に抽出したパラメータにより学習を試行することにより最適なパラメータを走査する方法です。
【メリット】
探索するパラメータの候補を把握しやすい
【デメリット】
組み合わせによる探索点の数が膨大になり得るため、探索するパラメータやその候補の数を多くすることができない
ベイズ最適化(Bayesian Optimization)
ベイズ最適化 (Bayesian Optimization) は、過去の実験結果から次の実験パラメータを、確率分布から求めることで最適化する手法です。
ランダムサーチではまったく精度が出なかったパラメータ付近も探索しますが、ベイズ最適化では探索履歴を使うことで精度が良い可能性の高いパラメータを効率良く探索することを試みます。
インストール
|
1 2 3 4 5 6 7 8 9 10 11 |
$ /c/Python38/Scripts/pip install bayesian-optimization Collecting bayesian-optimization Downloading https://files.pythonhosted.org/packages/72/0c/173ac467d0a53e33e41b 521e4ceba74a8ac7c7873d7b857a8fbdca88302d/bayesian-optimization-1.0.1.tar.gz Requirement already satisfied: numpy>=1.9.0 in c:\python38\lib\site-packages (from bayesian-optimization) (1.17.4) Requirement already satisfied: scipy>=0.14.0 in c:\python38\lib\site-packages (from bayesian-optimization) (1.4.1) Requirement already satisfied: scikit-learn>=0.18.0 in c:\python38\lib\site-packages (from bayesian-optimization) (0.2 2) Requirement already satisfied: joblib>=0.11 in c:\python38\lib\site-packages (from scikit-learn>=0.18.0->bayesian-opti mization) (0.14.1) Installing collected packages: bayesian-optimization Running setup.py install for bayesian-optimization: started Running setup.py install for bayesian-optimization: finished with status 'done' Successfully installed bayesian-optimization-1.0.1 |
実装方法
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
categorical_features = ["grade", "view", "waterfront"] def bayes_parameter_opt_lgb(X, y, init_round=15, opt_round=25, n_folds=5, random_seed=6, n_estimators=10000, learning_rate=0.05, output_process=False): # prepare data train_data = lgb.Dataset(data=X, label=y, categorical_feature = categorical_features, free_raw_data=False) # parameters def lgb_eval(num_leaves, feature_fraction, bagging_fraction, max_depth, lambda_l1, lambda_l2, min_split_gain, min_child_weight): params = {'application':'binary','num_iterations': n_estimators, 'learning_rate':learning_rate, 'early_stopping_round':100, 'metric':'auc'} params["num_leaves"] = int(round(num_leaves)) params['feature_fraction'] = max(min(feature_fraction, 1), 0) params['bagging_fraction'] = max(min(bagging_fraction, 1), 0) params['max_depth'] = int(round(max_depth)) params['lambda_l1'] = max(lambda_l1, 0) params['lambda_l2'] = max(lambda_l2, 0) params['min_split_gain'] = min_split_gain params['min_child_weight'] = min_child_weight cv_result = lgb.cv(params, train_data, nfold=n_folds, seed=random_seed, stratified=True, verbose_eval =200, metrics=['auc']) return max(cv_result['auc-mean']) # range lgbBO = BayesianOptimization(lgb_eval, {'num_leaves': (24, 45), 'feature_fraction': (0.1, 0.9), 'bagging_fraction': (0.8, 1), 'max_depth': (5, 8.99), 'lambda_l1': (0, 5), 'lambda_l2': (0, 3), 'min_split_gain': (0.001, 0.1), 'min_child_weight': (5, 50)}, random_state=0) # optimize lgbBO.maximize(init_points=init_round, n_iter=opt_round) # output optimization process if output_process==True: lgbBO.points_to_csv("bayes_opt_result.csv") # return best parameters return lgbBO.res['max']['max_params'] |
ベイズ最適化でのパラメータ探索
最近では hyperoptというライブラリが比較的よく使われています。
また2018年にoptunaというライブラリが公開されました。
hyperopt(ハイパーオプト)
TPE(tree-structured parzen estimator) というアルゴリズムで計算します。
次の設定をすることで、パラメータの探索を自動的に行い、探索したパラメータとそのときの評価指標によるスコアを出力できます。
- 最小化したい評価指標の設定
- 探索するパラメータの範囲を定義する
- 探索回数の指定
optuna(オプチュナ)
2018年末に公開されたフレームワークです。
開発会社は「Preferred Networks」。Chainerの生みの会社です。
最適化アルゴリズム自体はhyperoptと同様にTPEを用いていますが、次のような改善がされています。
- Define by Run スタイルAPI
- 学習曲線を用いた試行の枝刈り
- 並列分散最適化
何のパラメータを学習させるか?
重要と思われるパラメータからチューニングします。重要とされる順序は次のとおりです。
| max_depth | 決定木の深さ |
|---|---|
| subsample | 決定木ごとに学習データの行をサンプリングする割合 |
| colsample_bytree | 決定木ごとに特徴量の列をサンプリングする割合 |
| min_child_weight | 葉を分岐するために最低限必要となる葉を構成するデータ数 |
| gamma | 決定木を分岐させるために最低限減らさなくてはいけない目的関数の値 |
| alpha | 決定木の葉のウェイトに対するL1正則化の強さ |
| lambda | 決定木の葉のウェイトに対するL2正則化の強さ |
その他、パラメータには特徴があります。
モデル訓練のスピードをあげる
- bagging_fraction(初期値1.0)とbagging_freq(初期値0)を使う
- feature_fraction(初期値1.0)で特徴量のサブサンプリングを指定
- 小さいmax_bin(初期値 255)を使う
- save_binary(初期値 False)を使う
- 分散学習を使う
推測精度を向上させる
- 大きいmax_bin(初期値255)を使う
- 小さいlearning_rate(初期値0.1)と大きいnum_iterations(初期値100)を使う
- 大きいnum_leaves(初期値31)を使う
- 訓練データのレコード数を増やす(可能であれば)
過学習対策
- 小さいmax_binを使う(初期値255)
- 小さいnum_leavesを使う(初期値31)
- min_data_in_leaf(初期値20)とmin_sum_hessian_in_leaf(初期値1e-3)を使う
- bagging_fraction(初期値1.0)とbagging_freq(初期値0)を使う
- feature_fraction(初期値1.0)で特徴量のサブサンプリングを指定
- 訓練データのレコード数を増やす(可能であれば)
- lambda_l1(初期値0.0)、lambda_l2(初期値0.0)、min_gain_to_split(初期値0.0)で正則化を試す
- max_depth(初期値-1)を指定して決定木が深くならないよう調整する
optunaを使った実装内容
前回、KFoldやAUC、交差検証も取り入れたので、それらを全て含めたクラスを定義しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
import optuna import numpy as np import pandas as pd from lightgbm import LGBMClassifier from sklearn.metrics import roc_auc_score from sklearn.model_selection import KFold, StratifiedKFold # Optuna(ハイパーパラメータ自動最適化ツール) class Objective: def __init__(self, x, y, excluded_feats, num_folds = 4, stratified = False): self.x = x self.y = y self.excluded_feats = excluded_feats self.stratified = stratified self.num_folds = num_folds def __call__(self, trial): df_train = self.x y = self.y excluded_feats = self.excluded_feats stratified = self.stratified num_folds = self.num_folds # Cross validation model if stratified: folds = StratifiedKFold(n_splits = num_folds, shuffle = True, random_state = 1001) else: folds = KFold(n_splits = num_folds, shuffle = True, random_state = 1001) oof_preds = np.zeros(df_train.shape[0]) feats = [f for f in df_train.columns if f not in excluded_feats] for n_fold, (train_idx, valid_idx) in enumerate(folds.split(df_train[feats], y)): X_train, y_train = df_train[feats].iloc[train_idx], y.iloc[train_idx] X_valid, y_valid = df_train[feats].iloc[valid_idx], y.iloc[valid_idx] clf = LGBMClassifier(objective = 'binary', reg_alpha = trial.suggest_loguniform('reg_alpha', 1e-4, 100.0), reg_lambda = trial.suggest_loguniform('reg_lambda', 1e-4, 100.0), num_leaves = trial.suggest_int('num_leaves', 10, 40), silent = True) # trainとvalidを指定し学習 clf.fit(X_train, y_train, eval_set = [(X_train, y_train), (X_valid, y_valid)], eval_metric = 'auc', verbose = 0, early_stopping_rounds = 200) oof_preds[valid_idx] = clf.predict_proba(X_valid, num_iteration = clf.best_iteration_)[:, 1] accuracy = roc_auc_score(y, oof_preds) return 1.0 - accuracy def get_target_value(df): # 予測値(3日後の始値の上昇値) df['target'] = (df['open'].shift(-3) - df['open'].shift(-1)) / df['open'].shift(-1) df.loc[(df['target'] > 0.03), 'target'] = 1 df.loc[(-0.03 > df['target']), 'target'] = 0 return df if __name__ == '__main__': df_train = pd.read_csv("tosho/7203.csv", skiprows=0, skipfooter=0, engine="python", names=("date", "open", "high", "low", "close", "volume")) df_train = get_target_value(df_train ) df_train = df_train.dropna(subset=["target"]) df_train = df_train[(df_train['target'] == 1) | (df_train['target'] == 0)] excluded_feats = ['target', 'date'] # ハイパーパラメータ探索 objective = Objective(x=df_train, y=df_train['target'], excluded_feats=excluded_feats, num_folds = 5, stratified = True) study = optuna.create_study(sampler = optuna.samplers.RandomSampler(seed = 0)) study.optimize(objective, n_trials = 50) |
結果は次のようになっています。
|
1 2 3 4 |
[I 2020-02-13 08:54:40,769] Finished trial#0 resulted in value: 0.4242554162931452. Current best value is 0.4242554162931452 with parameters: {'reg_alpha': 0.19628224813442816, 'reg_lambda': 1.9549524484259886, 'num_leaves': 13}. [I 2020-02-13 08:54:41,585] Finished trial#1 resulted in value: 0.4176141583656743. Current best value is 0.4176141583656743 with parameters: {'reg_alpha': 0.022735723377092197, 'reg_lambda': 10.386580256500284, 'num_leaves': 18}. .... [I 2020-02-13 08:55:25,740] Finished trial#49 resulted in value: 0.42349120530966555. Current best value is 0.40829885799874166 with parameters: {'reg_alpha': 0.053599319721492705, 'reg_lambda': 67.99782871248236, 'num_leaves': 40}. |
出力されたパラメーターを使って実際に学習させてみます。
|
1 2 3 4 5 |
# LightGBM clf = LGBMClassifier(reg_alpha = 0.44004414216369864, reg_lambda = 0.07343092808809583, num_leaves = 29) # trainとvalidを指定し学習 |
|
1 2 3 4 |
7203 Starting cross_validation. Train shape: (1201, 22), test shape: (5409, 21) Full AUC score 0.689215 [0.30833605 0.28220892 0.27507515 ... 0.32182241 0.34561377 0.50051291] |
AUCの出力は「0.69」です。
実際には精度が上がる銘柄と上がらない銘柄がありました。
max_depthを指定して過学習を防いでみる
「max_depth=4」を指定してLightGBMを解いてみます。
作られた決定木です。
これぐらいの木であれば過学習は避けられているかもしれません。
因みに「AUC=0.65」程度でした。
下がりましたが、前回スコアを0.7まで上げていたので昔の値に戻った程度です。
なお「1998/01/05~2015/12/14」を利用して学習させています。
つまり「2015/12/15~2020/01/24」が未知の予測(フォワードテスト)となります。
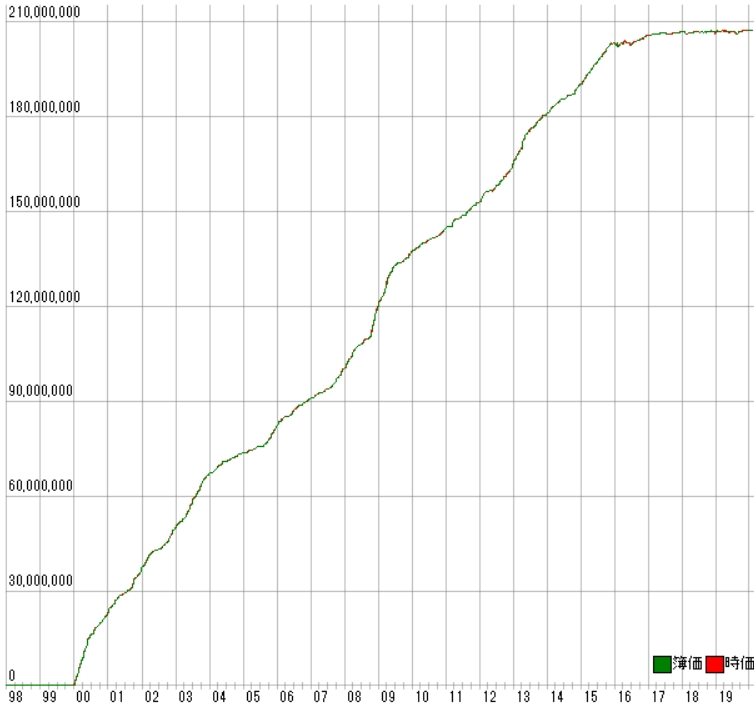
その結果です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
株価データ: 日足 銘柄リスト: 日経225採用銘柄 1998/01/05~2020/02/14における成績です。 ---------------------------------------- 全トレード数 7269 勝ちトレード数(勝率) 5357(73.70%) 負けトレード数(負率) 1912(26.30%) 全トレード平均利率 3.09% 勝ちトレード平均利率 4.88% 負けトレード平均損率 -1.94% 勝ちトレード最大利率 85.07% 負けトレード最大損率 -13.97% 全トレード平均期間 4.44 勝ちトレード平均期間 4.43 負けトレード平均期間 4.44 ---------------------------------------- 必要資金 ¥9,976,900 最大ポジション(簿価) ¥9,997,900 最大ポジション(時価) ¥11,823,600 純利益 ¥207,281,100 勝ちトレード総利益 ¥240,597,300 負けトレード総損失 -¥33,316,270 全トレード平均利益 ¥28,516 勝ちトレード平均利益 ¥44,913 負けトレード平均損失 -¥17,425 勝ちトレード最大利益 ¥797,500 負けトレード最大損失 -¥129,600 プロフィットファクター 7.22 最大ドローダウン(簿価) -¥1,407,968 最大ドローダウン(時価) -¥1,636,608 ---------------------------------------- 現在進行中のトレード数 0 ---------------------------------------- 平均年利 98.93% 平均年利(直近5年) 7.56% 最大連勝 33回 最大連敗 8回 ---------------------------------------- [年度別レポート] 年度 取引回数 運用損益 年利 勝率 PF 最大DD 2020年 45回 -¥238,900円 -2.39% 37.78% 0.53倍 -5.27% 2019年 514回 ¥954,900円 9.57% 54.67% 1.20倍 -10.43% 2018年 472回 -¥483,300円 -4.84% 49.58% 0.90倍 -13.06% 2017年 494回 ¥1,165,100円 11.68% 55.47% 1.38倍 -6.98% 2016年 629回 ¥2,372,400円 23.78% 53.26% 1.29倍 -13.97% 2015年 525回 ¥12,996,000円 130.26% 77.71% 9.09倍 -5.07% 2014年 325回 ¥9,181,900円 92.03% 79.08% 10.14倍 -5.63% 2013年 435回 ¥15,987,500円 160.25% 82.99% 15.71倍 -6.75% 2012年 433回 ¥12,356,400円 123.85% 77.83% 9.82倍 -4.59% 2011年 246回 ¥8,249,500円 82.69% 84.55% 15.91倍 -4.23% 2010年 285回 ¥7,295,700円 73.13% 80.70% 9.04倍 -6.90% 2009年 326回 ¥16,984,600円 170.24% 85.89% 21.34倍 -7.58% 2008年 320回 ¥19,998,300円 200.45% 92.19% 36.55倍 -11.74% 2007年 262回 ¥9,402,500円 94.24% 88.17% 22.73倍 -5.67% 2006年 251回 ¥8,826,400円 88.47% 82.07% 15.88倍 -10.34% 2005年 228回 ¥8,600,800円 86.21% 86.40% 25.11倍 -3.90% 2004年 191回 ¥6,512,900円 65.28% 82.72% 12.81倍 -8.82% 2003年 338回 ¥17,201,800円 172.42% 89.05% 42.56倍 -4.09% 2002年 268回 ¥12,570,700円 126.00% 88.06% 29.07倍 -3.27% 2001年 287回 ¥14,371,800円 144.05% 86.76% 25.50倍 -5.81% 2000年 395回 ¥22,974,300円 230.27% 89.87% 45.68倍 -3.74% |
利益曲線は次のとおりです。
前回同様、フォワードテスト後に寝ています。
決定木を4階層にすることで、勝率、プロフィットファクターは下がりましたがフォワードテストの勝率が少しだけ改善しました。
誤差の範囲かもしれませんが、多少の自動売買の活路がみえました。
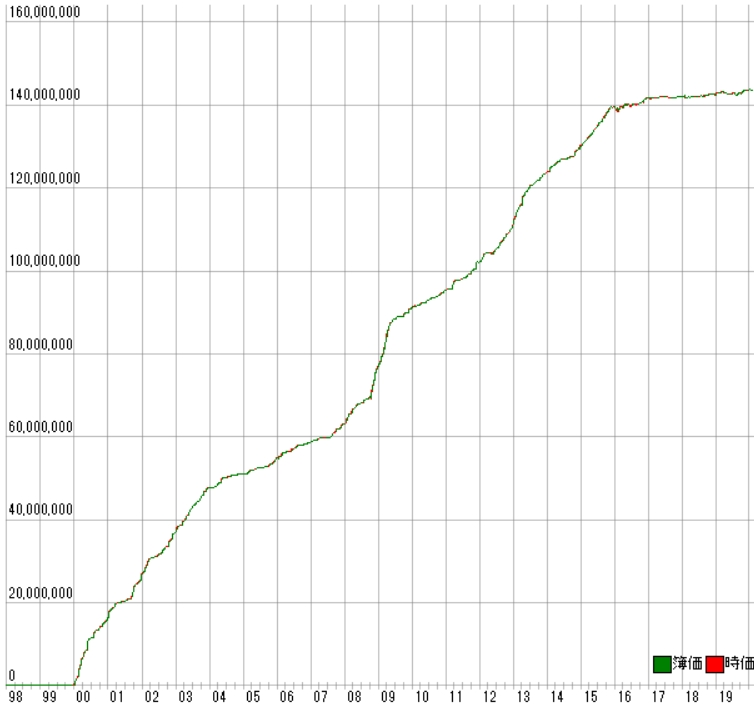
ちなみに「max_depth=3」の場合は次の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
全トレード数 5118 勝ちトレード数(勝率) 3729(72.86%) 負けトレード数(負率) 1389(27.14%) 純利益 ¥143,632,800 プロフィットファクター 6.87 平均年利 70.78% 平均年利(直近5年) 8.37% ---------------------------------------- [年度別レポート] 年度 取引回数 運用損益 年利 勝率 PF 最大DD 2020年 35回 -¥21,000円 -0.22% 60.00% 0.93倍 -5.71% 2019年 397回 ¥1,323,500円 13.70% 55.16% 1.40倍 -11.63% 2018年 324回 ¥166,100円 1.72% 51.85% 1.05倍 -10.58% 2017年 355回 ¥509,100円 5.27% 54.93% 1.22倍 -6.98% 2016年 531回 ¥2,065,900円 21.38% 54.05% 1.33倍 -12.66% 2015年 388回 ¥9,353,200円 96.79% 78.09% 9.02倍 -5.13% 2014年 208回 ¥6,372,300円 65.95% 84.13% 13.06倍 -5.40% 2013年 304回 ¥12,330,800円 127.61% 84.87% 21.07倍 -4.00% 2012年 352回 ¥9,451,000円 97.81% 76.14% 8.77倍 -6.80% 2011年 176回 ¥6,643,600円 68.75% 80.68% 13.49倍 -4.44% 2010年 149回 ¥4,257,000円 44.05% 81.21% 11.15倍 -3.81% 2009年 259回 ¥14,073,200円 145.64% 83.01% 16.30倍 -7.58% 2008年 229回 ¥13,998,300円 144.87% 89.08% 18.55倍 -12.69% 2007年 128回 ¥4,207,200円 43.54% 87.50% 19.93倍 -3.47% 2006年 126回 ¥4,041,000円 41.82% 78.57% 9.26倍 -6.20% 2005年 96回 ¥3,661,700円 37.89% 85.42% 20.69倍 -7.82% 2004年 92回 ¥3,572,600円 36.97% 84.78% 14.46倍 -4.20% 2003年 222回 ¥10,508,400円 108.75% 88.29% 37.16倍 -4.78% 2002年 214回 ¥10,475,700円 108.41% 88.32% 32.11倍 -5.68% 2001年 222回 ¥10,136,900円 104.90% 81.98% 15.97倍 -7.33% 2000年 311回 ¥16,506,300円 170.82% 87.78% 31.52倍 -4.44% |
利益曲線は次のとおりです。
「max_depth=4」の場合と大きな差はありません。
これ以上の深さの変更には意味は無さそうです。
まとめ
Optunaでパラメータチューニングは、一度実装できれば非常に簡単に出来ることが分かりました。
しかしパラメータを変更すると、逆に精度が落ちてしまうこともあり、非常に使い辛いです。
また株価予測でチューニングすべきは過学習にならない為であり、そのためには「max_depth」に多少の価値があることが分かりました。