小学生を子にもつ親子必見の漫画「二月の勝者」のドラマ第一話。
© 二月の勝者-絶対合格の教室/高瀬志帆/小学館/日本テレビ

私が このボールを手から離します。
どうなりますか?
(王羅) 床に落ちるに決まってんじゃん。

そうですか。
(華鈴) そんなの常識じゃん。
(真千音) 絶対 落ちるよ。

では こういう考えがあります。
ボールは床に落ちる時
必ず まず この高さの半分まで落ちる。
この考えは正しいですか?間違ってますか?
(花恋) 別に 正しいんじゃない?

あなたはΩクラスのエース
前田花恋さん。
(勇人) エースだってウケるんですけど。

では 前田さん。半分まで落ちた後
ボールは また残りの高さの半分まで落ちる。
次に また その半分落ちる。
この考えは正しいですか?
(花恋) そりゃ落ちる時に そうなるっしょ。

絶対ですか?
(花恋) 絶対だよ。

でも 考えてみてください。
この半分落ちる半分落ちるを繰り返して行くと
ボールは いつまでたっても床に到着することができない。
つまり 床に落ちるのは不可能だ。ということになりませんか。
しかし 実際にやってみると…。
ボールは床に落ちた。

頭で考えただけでは不可能だと思っていても
実際にやってみないと分からない。
やってみれば可能なこともあるんです。
あり得ないなんてことはない。
不可能を可能にする。
それが中学受験です。
いや、そのりくつはおかしい。
© ドラえもん/藤子・F・不二雄/小学館
意味分かんねーよ!
どう中学受験の話と繋がるんだよww
パラドックスと合格の可能性を一緒にするなんて、単なる詐欺師の手口だろww
安っぽいオリジナル・ストーリーを追加するんじゃないよ!
そもそも、有名な逸話だからΩクラス生が誰も知らない訳がない。
私が この問題を知ったのは高校一年生の時だけどね。
不合理だとわかっていても、なかなか論破できない主張のたとえ。
広島駅前の河合塾数学講師 鈴木氏が「昔、東大で出題された問題」だと授業中に紹介してくれた。
改めて数学の問題として考えてみよう。
そもそも「アキレスと亀(カメ)」とは、どんな問題か?
古代ギリシャの哲学者、アリストテレスの「自然学」の中で紹介されている、哲学者ゼノンが提示したパラドックスの一つ。
俊足で有名な英雄「アキレス」と「カメ」の競争話だけど、ここでは「ウサギ」を「カメ」で説明する。
ウサギとカメが競争する。
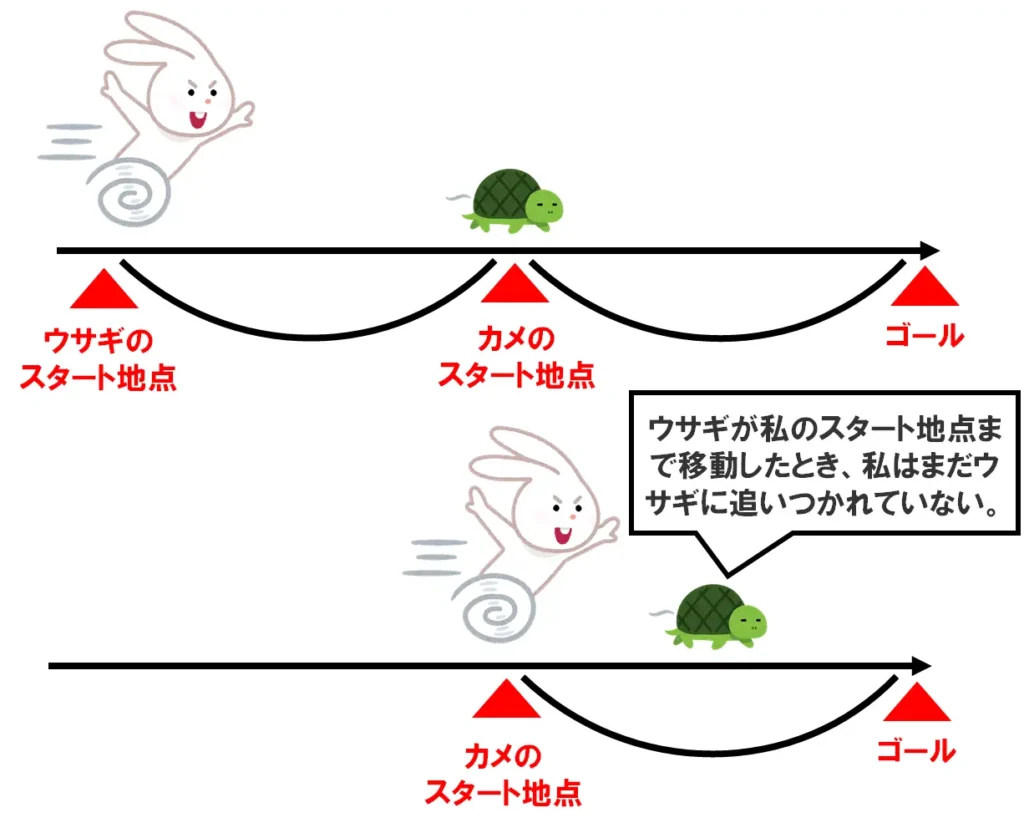
ただし、ウサギの方が早いのでハンデとしてカメはゴールまでの地点の半分からスタートする。
両者同時にスタートして、ウサギがカメのスタート地点まで移動したときカメはまだウサギに追いつかれない。
次にウサギから見て今前方にいるカメの位置まで移動したとき、カメはこの間にまたわずかにゴールに近づいているのでまだウサギには追いつかれない。
これを繰り返し考えていくと前を走っているカメにウサギは追いつけないことになる。
この矛盾を数学的に証明せよ。
これに対する返答をググって最初に検索ヒットしたのは「教えてGoo」。
追いつけないのは、いつまでですか?
それともどこまでですか?
「いつまで」「どこまで」という仮定を書かずに曖昧にしているのが混乱の原因です。

んな事は講釈垂れずとも誰でも分かってんだよ!
あんた、勉強できねーだろ?
解答用紙にそう書くのかよwww
もう、知恵袋系のサイトは廃止で良いんじゃない?
返答者のレベルが低くて何一つ解決した事ないわww
この問題は、既に「数学」「論理学」「哲学」それぞれで答えが出ている。
数字を使った一般的な解法
カメのいた位置にウサギがたどり着いたときに、カメは少し前にいる。
その少し前にいるカメの位置まで、ウサギが到着したときには、カメはやはり少し前にいる。
以降これの繰り返しが無限に続く。
無限級数を持ち出すまでもなく、小学生や中学生で勉強する、「速さの問題」の考え方を用いても同様に追いつく時間と、追いつく地点を求めることが可能。
まずはそちらを紹介する。
旅人算で考えてみる(小学生編)
受験を目指す小学生は「旅人算」を学ぶ。
カメが速さ 0.5m/秒 で出発し、10秒後に、ウサギが速さ 1m/秒 で追いかけた。
このとき、ウサギがカメ追いつくまでの時間を求めよ。
【回答】
ウサギが出発する時のカメとの距離
= カメの速さ×出る時間差
= 0.5m/秒 × 10秒
= 5 m
ウサギが追いつくまでの時間
= ウサギが出発する時のカメとの距離÷(ウサギの速さ−カメの速さ)
= 5m ÷ (1m/秒 – 0.5m/秒)
= 10秒
要するに10秒走った瞬間にウサギとカメの両者は並び、つぎの瞬間に追い越す。
無限等比級数で考えてみる(高校生編)
ウサギが90m 先にいるカメと競走をするとする。
- ウサギが90m 進んだときに、カメは9m先にいる
- ウサギが9m 進んだときに、カメは0.9m先にいる
- ウサギが0.9m進んだときに、カメは0.09m先にいる
これを元に、ウサギの進んだ距離Xを式で表すと、
![]()
となる。
となり、99.999999…m 地点で追いつく。
これは等比数列の和であり、この足し算を無限回行うという無限等比級数の概念を用いると次のようになる。
![]()
よってX は100 に収束することになる。
つまり、100m の地点において、ウサギはカメに追いつくという計算になる。
数列![]() に対して、初項から順に
に対して、初項から順に
![]()
と無限に足していったときの極限を![]() と表し、これを無限級数という。
と表し、これを無限級数という。
![]()
また、数列![]() が等比数列のとき、
が等比数列のとき、![]() の無限級数
の無限級数![]() を無限等比級数という。
を無限等比級数という。
また、追いつく時刻Tについては、ウサギが90mを9秒で進むと考えると、
![]()
ということになる。
これもまた、無限等比級数であり、
![]()
となるので、スタートから10秒後に追いつく。
よって、カメとウサギの追いつき合戦が無限回行われた後、ウサギが100m、10秒走った瞬間に両者は並び、つぎの瞬間に追い越す。
「アキレスとカメ」の話は「10秒=9.999999…秒」を逆手に取り、「アキレスはカメに追いつくのに無限秒かかる」と説明しているのに過ぎない。
つまり「9.99よりも大きな9.999よりも大きな9.9999…と話は無限回続く」という回数の無限と「いつまで経っても」という時間や距離の無限を混同しているのが問題。
まとめ
ゼノンはアキレスとカメが進行し続けるという無限の繰り返しに注意を向けさせることによって、分割的無限(相対距離は有限)の話を、延長的無限(どこまでも延長されて無限に続く)の話にすり替えている。
つまり有限性を忘れさせることによる錯覚。
数学的な考え方だと、ウサギとカメの追いつき合戦は無限スッテプ行われる。けれど、それにかかる時間と距離は有限であるから、追いつくことができる。
そして、それは無限ステップ目で追いつく。