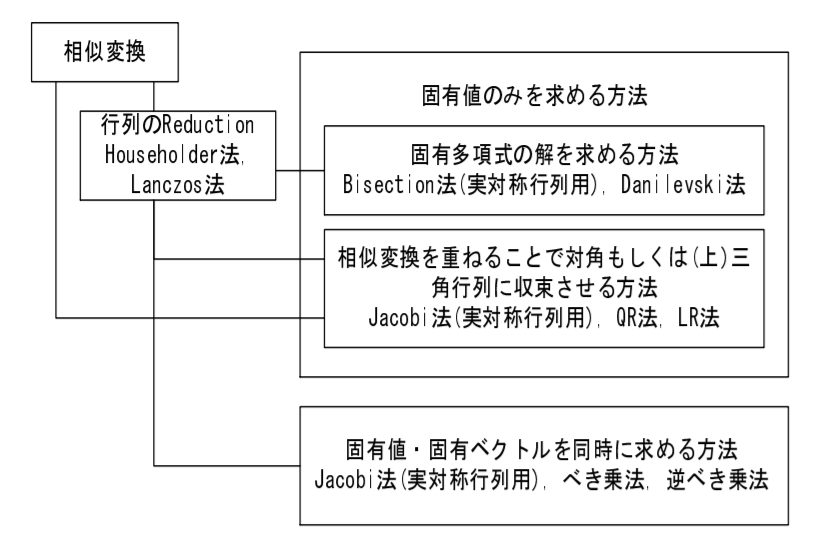
最大固有値とその固有ベクトルを求める方法としては、ベキ乗法(power iteration)がある。
学生時代に「第3回アルゴリズムコンテスト(’99)「カメレオンはどこだ! −テクスチャ画像の領域分割−」の宿題があり、提出したレポートの抜粋。
実験例
図1に示すclass1とclass2の画像を同一の手法で対象領域と背景領域に分割し、2値画像(黒白画像)を生成してみる。
図1 class1の画像(上)とclass2の画像(下)
多機能性をもつ手法
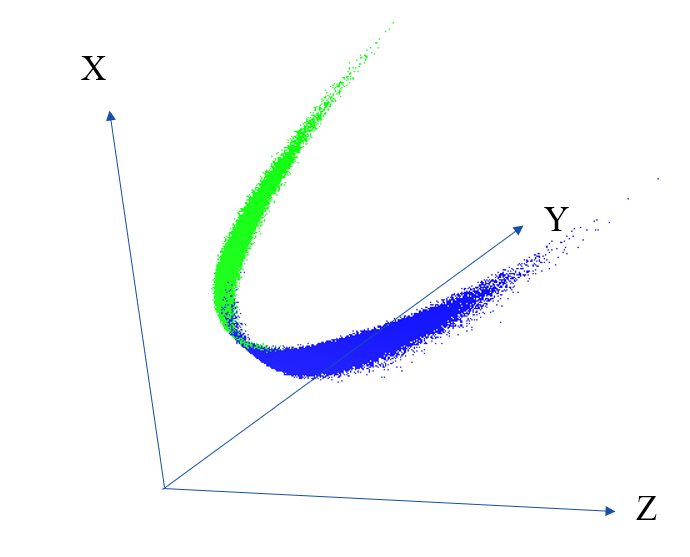
濃淡ヒストグラムをx軸、y軸、z軸…とおき、多次元空間中で分割面を決定し2値画像を生成する。
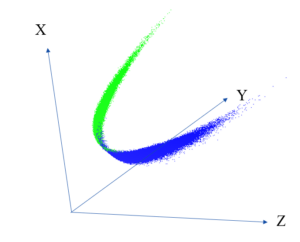
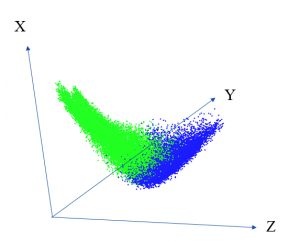
3次元空間中にプロットした例を図2、3に示す。
ここで、黄緑色が物体領域、青色が背景領域である(左のクラスが物体領域、右のクラスが背景領域)。
図2 平均、コントラスト、分散を軸とした3次元グラフ(class1)
図3 分散、エネルギー、エントロピーを軸とした3次元グラフ(class2)
3次元空間の場合、点群の共分散行列を次のように定義する。
(1) 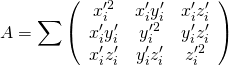
ただし、
![]()
![]()
![]()
である。
この最大固有ベクトルを、![]() とし、この軸への投影を、
とし、この軸への投影を、
(2) ![]()
とする。
![]() にたいして 大津の閾値 の手法で閾値
にたいして 大津の閾値 の手法で閾値![]() を決める。
を決める。
すなわち、単位ベクトル![]() を用いると、次の判別式で2値化する事になる。
を用いると、次の判別式で2値化する事になる。
(3) 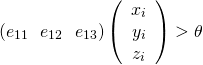
アルゴリズム設計
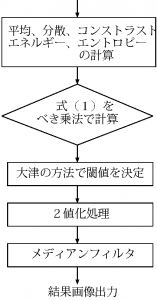
設計したアルゴリズムを図4に示す。
対象と背景を分割するアルゴリズム
まず、あらかじめ平均(mean)、コントラスト(contrast)、分散(variance) 、エネルギー(energy)、エントロピー(entropy)を計算しておく。
次に5×5行列に拡張した式(1)を解き、最大固有ベクトルを求め閾値を求め、2値化処理を行う。
実験結果
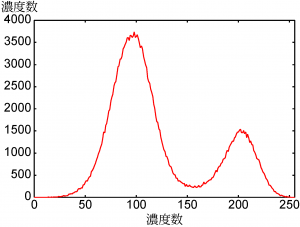
class1の結果のヒストグラムを図5に、class2の結果のヒストグラムを図6に示す。
図5 class1のヒストグラム
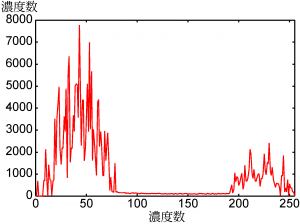
図6 class2のヒストグラム
本手法で得られたclass1とclass2の2値化結果を図7、図8に示す。
図7 class1の画像結果
図8 class2の画像結果
精度評価
得られた2つの画像の精度の評価を行う。今回は正解画像が提供されているため、正解画像と出力画像との誤り画素数を計測する。
メディアンフィルタを用いる前の精度結果を表1に示す。
表1 本手法で得られた画像の精度
| 画像 | 正解画像との画素誤り(画素) | 正解画像との画素誤り |
|---|---|---|
| class1 | 6046 | 2.306 |
| class2 | 6125 | 2.337 |
表1より本手法を適用した結果、class1、class2共に約![]() の精度が得られた。
の精度が得られた。
次にこの結果にメディアンフィルタを用いた結果を図9、図10に示す。
また、精度結果は表2に示す。
図9 class1の画像結果
図10 class2の画像結果
表2 メディアンフィルタを用いた結果
| 画像 | 正解画像との画素誤り(画素) | 正解画像との画素誤り |
|---|---|---|
| class1 | 4046 | 1.543 |
| class2 | 5688 | 2.170 |
表2より、メディアンフィルタが最後の処理として有効であることが分かる。
ソース
以下に作成したソース(必要であろうと思われる箇所のみ)。
ライブラリ部分
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 |
class Matrix{ // 行列クラス public: double*p; int W, H; // 転置 static void Transpose(double *R, double *Q, int W, int H){ int i,j; for(i=0; i<H; ++i) for(j=0; j<W; ++j) Q[j*H+i] = R[i*W+j]; } // 外積 static void Cross(double r[], double x[], double y[]){ r[0] = x[1]*y[2]-x[2]*y[1]; r[1] = x[2]*y[0]-x[0]*y[2]; r[2] = x[0]*y[1]-x[1]*y[0]; } // X=X+aY static void VSA(double X[], double a, double Y[], int T){ int i; for(i=0; i<T; ++i) X[i]+=a*Y[i]; } // 内積 static double Dot(double R[], double Q[], int x=3){ int i; double k=0; for(i=0; i<x; ++i) k+=R[i]*Q[i]; return k; } //単位ベクトル k=|a| static double Normalize(double x[], int T=3){ double k=sqrt(Dot(x, x, T)), r=1/k; for(int i=0; i<T; ++i) x[i]*=r; // 書き換え return k; } // QR分解 A[][]=Q[][] static void QR(double A[][4], void*_AA, double R[][4], int T){ int i, k, j; double (*AA)[T]=(double(*)[T])_AA; Transpose(*A, *AA, 4, T); for(i=0; i<4; ++i) for(j=0; j<4; ++j) R[i][j]=0.0; for(j=0; j<4; j++){ for(k=0; k<j; k++){ VSA(AA[j], -(R[k][j]=Dot(AA[j], AA[k], T)), AA[k], T); } R[j][j]=Normalize(AA[j], T); } // Transpose(*AA, *A, T, 4); } // 後退代入(QR分解とセット) static void Backward(double R[][4], double M[], double O[]){ double k=0; int i,j; for(i=4; i--;){ k=0; for(j=3; j>i; --j) k-=R[i][j]*O[j]; O[i]=(M[i]+k)/R[i][i]; } } // ベキ乗法を求める -> 最大固有値を求める static void Power(double out[], void*_A,int T=3){ int max=100; // 反復回数上限を設定 double xi=.0; // 固有値 double x[T]; // あたかも2次元配列のように見える double (*A)[T]=(double(*)[T])_A; for(int i=0; i<T; i++) out[i]=1/sqrt(T); // 正規化(2乗して総和が1) for(int i=0; i<max; i++){ for(int j=0; j<T; j++) x[j]=Dot(A[j], out); xi=Normalize(x); // 固有ベクトルはノルムが1となるように正規化 // fprintf(stderr, "i=%2d : %f (%f %f %f)\n",i,xi,out[0],out[1],out[2]); int j=0; for(; j<T; j++){ double t=out[j]-x[j]; if(t*t>1e-20) break; // 閾値 } if(j==T) return; for(int j=0; j<T; j++) out[j]=x[j]; } throw "ベキ乗法は収束しない"; } }Matrix; class MairicRec : public Matrix{ public: // 4元数を求める <- 入力 Q(q_0, q_1, q_2, q_3) static void Quat(double *r, double *q){ r[0]=q[0]*q[0]+q[1]*q[1]-q[2]*q[2]-q[3]*q[3]; r[1]=2*(q[1]*q[2]-q[0]*q[3]); r[2]=2*(q[1]*q[3]+q[0]*q[2]); r[3]=2*(q[1]*q[2]+q[0]*q[3]); r[4]=q[0]*q[0]-q[1]*q[1]+q[2]*q[2]-q[3]*q[3]; r[5]=2*(q[2]*q[3]+q[0]*q[1]); r[6]=2*(q[1]*q[3]+q[0]*q[2]); r[7]=2*(q[2]*q[3]+q[0]*q[1]); r[8]=q[0]*q[0]-q[1]*q[1]-q[2]*q[2]+q[3]*q[3]; } }; |
メイン部分
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 |
/******** 画像の平均化、コントラスト、分散化 、歪度、尖度 ********/ { for(j=B;j<512-B;j++) for(i=B;i<512-B;i++){ double men=0,cnt=0,var=0,skw=0,krt=0; for(y=-B;y<B;y++) for(x=-B;x<B;x++){ men+=inImage[j+y][i+x]; cnt+=inImage[j+y][i+x]*inImage[j+y][i+x]; } men=men/(4*B*B); cnt=cnt/(4*B*B); for(y=-B;y<B;y++) for(x=-B;x<B;x++){ t=inImage[j+y][i+x]-men; var+=t*t; skw+=t*t*t; krt+=t*t*t*t; } var=var/(4*B*B); skw=(skw*skw/(4*B*B*4*B*B*var*var*var)); krt=krt/(4*B*B*var*var); } } /******** 画像のエネルギー、エントロピー ********/ { for(j=B;j<512-B;j++) for(i=B;i<512-B;i++){ double egy=0,epy=0; int hist[256]; for(x=0;x<256;x++) hist[x]=0; // 初期化 for(y=-B;y<=B;y++) for(x=-B;x<=B;x++) hist[inImage[j+y][i+x]]++; // ヒストグラムの作成 for(x=0;x<256;x++){ egy+=hist[x]*hist[x]; if(hist[x]) epy+=hist[x]*log(hist[x]); } egy=egy/(4*B*B+1+4*B); epy=epy/(4*B*B+1+4*B); } } /******** オイルペインティング・メディアンフィルタの実装 ********/ { #define oil 3 #define area (2*oil+1)*(2*oil+1) int a[area+1],flag=0; for(j=oil; j<512-oil; j++) for(i=oil; i<512-oil; i++){ /* Insertion sort */ flag=0; for(y=-oil; y<=oil; y++) for(x=-oil; x<=oil; x++){ int s,t=inImage[j+y][i+x]; for(s=flag;s && a[s-1]>t;s--) a[s]=a[s-1]; a[s]=t; flag++; } /* Select most frequently used level オイルペインティング */ { int max=0, cnt=1, t=a[0], mt; a[area]=-1; for(y=1; y<area+1; y++){ if(t==a[y]) cnt++; else{ if(max<=cnt) max=cnt, mt=t; cnt=1; t=a[y]; } } outImage[j][i] = mt; } /* median filter メディアンフィルタ */ { outImage[j][i] = a[(int)(area/2)]; } } } Main(){ if(ac>1 && 0==strcmp(av[1],"--help")){ printf("ベキ乗法を求めるプログラム\n"); exit(1); } int max=0; double A[3][3]; double (*s)[3]=new double[999999][3]; int t=0; for(int i=0; i<3; i++) for(int j=0; j<3; j++) A[i][j]=.0; // init double x,y,z,c; for(int i=0; EOF!=scanf("%lf %lf %lf %x",&x,&y,&z,&c); i++){ max++; s[i][0]=x; s[i][1]=y; s[i][2]=z; A[0][0]+=x*x; A[0][1]+=x*y; A[0][2]+=x*z; A[1][0]+=x*y; A[1][1]+=y*y; A[1][2]+=y*z; A[2][0]+=x*z; A[2][1]+=y*z; A[2][2]+=z*z; } for(int i=0; i<3; i++){ for(int j=0; j<3; j++) fprintf(stderr, "%f ",A[i][j]); fprintf(stderr, "\n"); } fprintf(stderr, "-----\n"); double xi[3],u[max]; Matrix.Power(xi, A); for(int i=0; i<max; i++){ u[i]=Matrix.Dot(s[i], xi); printf("%f\n",u[i]); } delete[] s; } |