久しぶりに、同学科で一足先に社会人になった輩と飲みに行った。
てか社会人毎日お手洗いにも行かず、昼から夕方まで席を立つことが無いとか・・
今の怠惰な生活だと、10分も椅子に座れません。私・・・
しかも今残業中の輩も・・・今日は土曜日・・PM11時なんだけど・・

君たち頑張りすぎ・・・
◇
先日、Mr.マリックとクリス・エンジェルの「超魔術頂上決戦!!」って番組がありましたね。
私のサイトではマジック関係もやっているので、大抵TV 番組の後は訪問者が増えます。
で、決まって届くメール・・・
○○のタネを教えて下さい。
てか、知らねぇし、TV 番組全て見てるわけではない!!
少なくとも・・・
人から借りたお金に火をつけたら消えて、砂時計の中から出てきたタネ教えて下さい!
と言うメールの質問は、後半の現象が間違っている。
砂時計のフタを開けて、砂の中にマリックが手を突っ込んでお札を取り出した。
これが、正しい。
重要なとこ見落としすぎです。手を突っ込んだなら色々方法があるんだよ、これが・・・
◇
つまり人間は、重要なことを見落としがちなのです。←こっちが本題。
一つ例を示しましょう。
ある高校のクラスには40人の生徒がいます。
その中で、誰かと誰かの誕生日が一致する可能性は何パーセント程度でしょう?
さて、どうでしょうか?
何人かに出した結果 10% 程度という解答が最も多かったですね。
確かに、自分とA さんの誕生日が一致する確率は、1/365です。
同様に自分とB さんの誕生日が一致する確率も、1/365です。
このため、自分と39 人の生徒の誕生日が一致する確率は、39/365であり、10% 程度となります。
しかし、
A さんとB さんの誕生日が一致する確率も 1/365
なのです。
自分と誰かの組み合わせは39 通りに過ぎなくても、任意の2 人の組み合わせは膨大な
数になります。
40 人から任意の2 人の組み合わせは、以下の式で求めることができます。
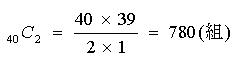
また、40 人のグループの中に2人以上誕生日が一致する確率 P は、全員の誕生日が
一致しない確率を求めて、1 から引く。
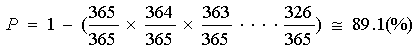
ただし、1 年を365 日としています。
つまり、
同じ誕生日の生徒が存在する確率は90%
という結果になります。
まあ、似た例として「虫のしらせ」や「幸福グッズ」なども計算すれば分かることなのだが・・・
日記でウンチクたれる必要もないわな。
よく聞く話だろうし、他のコンテンツにまわします。ここ