 2024年(社会人20年)
2024年(社会人20年) 完全無料で動画に口パク・字幕を自動追加する(AviUtl、GIMP、PSDToolKit、Subtitler)
大学生時代にはアルバイトでAdobe Premierを使って字幕付け&動画編集の経験がある(市町村合併前方言を残すプロジェクト)。
社会人になってからはAdobe Effectsのプラグインも購入し結婚式やテニス部の動画を作成してた。...
 2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  機械学習
機械学習 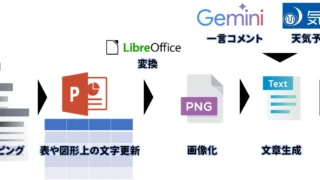 機械学習
機械学習 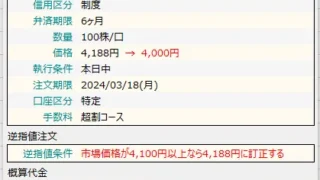 2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年) 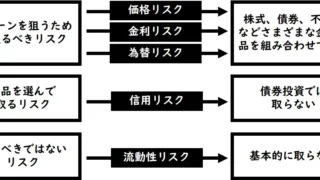 2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)  2024年(社会人20年)
2024年(社会人20年)